
|
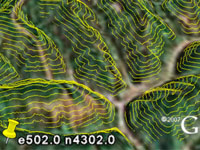
Visualizing LIDAR in Google Earth We provide streaming tools that allow fast visualization of LIDAR data in Google Earth. They are useful to quickly generate previews for large amount of LIDAR data either for rapid inspection and verification or for easy presentation within a geospatial context to a wide audience. For example, gilmer.kmz was created in 20 minutes using less than 100 MB main memory and no temporary disk space with the processing pipeline described here. The input were 357 LAS files (from West Virginia View) with a total 156 million LIDAR points. Another - more interesting - example is Mount Saint Helens. Inside the vulcano's cone the elevation of the Google Earth terrain is quite noticably out-of-date. executables & readme: tools, source code: sp_api.zip sm_api.zip sl_api.zip contour examples: gilmer.kmz saint_helens.kmz raster examples: fitchburg.kmz saint_helens.kmz grbm.kmz toronto.kmz gilmer.kmz |

|
LAStools: converting, filtering, viewing, processing, and compressing LIDAR data A set of simple command line tools for the standard LAS or the compressed LAZ format. There are tools for converting from/to ASCII or Shapefiles, for viewing, thinning, contouring, merging, filtering, TIN triangulating, DEM rasterizing, boundary polygon creation, ... We also provide an ultra-light weight C++ API called LASlib (with LASzip) for reading and writing of LIDAR from and to standard LAS or compressed LAZ. The source code is LGPL. LASlib (with LASzip): compressing LIDAR data in the binary LAS format A compressor laszip.exe and an ultra-light weight and very efficient C++ programming API called LASlib (with LASzip) for reading and writing LIDAR from and to standard LAS or compressed LAZ (versions 1.0-1.3). The compressed LAZ files are only around 10 - 20 percent of their original size without any loss. All source code (LGPL) is included. executable: laszip.exe API & source code: LASlib.zip |
|
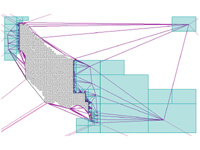
Generating Raster DEM from Mass Points via TIN Streaming It is difficult to generate raster Digital Elevation Models (DEMs) from terrain mass point data sets too large to fit into memory, such as those obtained by LIDAR. We describe prototype tools for streaming DEM generation that are based on Streaming Delaunay and that use memory and disk I/O very efficiently. From 500 million bare-earth LIDAR double precision points (11.2 GB) our tool can, in just over an hour on a standard laptop with two hard drives, produce a 50,394 x 30,500 raster DEM with 20 foot post spacing in 16 bit binary BIL format (3 GB), using less than 100 MB of main memory and less than 300 MB of temporary disk space. paper: ilsst-tin2dem-06.pdf slides: tin2dem.ppt (+vids) |
|
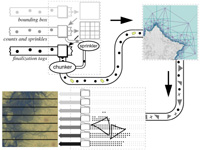
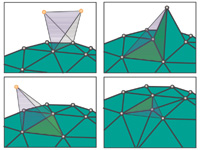
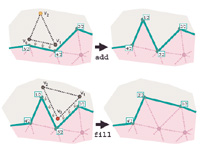
Streaming Delaunay We demonstrate how algorithms to compute Delaunay triangulations for large, well-distributed data sets in 2D and 3D can be greatly accelerated by exploiting the natural spatial coherence in a stream of points. We introduce spatial finalization for point streams: we partition the bounding box into regions, and augment the stream of input points with finalization tags that indicate when a point is the last in its region. By extending an incremental algorithm for Delaunay triangulation to use finalization tags and produce streaming mesh output, we compute a billion-triangle terrain representation for the Neuse River system from 11.2 GB of LIDAR data in 48 minutes using 70 MB of memory on a laptop. paper: ilss-scdt-06.pdf demo: sd_demo.zip API & source code: sp_api.zip video: sd_video.avi slides: sd.ppt (+vids) First Application: We use Streaming Delaunay to extract high-resolution iso-contour elevation lines from large amounts of terrain points (e.g. LIDAR data). Memory use is much less than processed input and produced output. paper: ils-lidar2iso-06.pdf demo: lidar2iso_demo.zip |
|
Streaming Compression of Tetrahedral Volume Meshes A streaming compression scheme for tetrahedral volume meshes that encodes vertices and tetrahedra in the order they are written. To keep the memory footprint low, the compressor is informed when vertices are referenced for the last time (i.e. are finalized). For reasonably coherent input and a reorder buffer of 10,000 tetrahedra, we achieve compression rates that are only 25 to 40 percent above the state-of-the-art, while requiring drastically less memory resources and less than half the processing time. paper: ilgs-sctvm-06.pdf source code: sv_api.zip demo: sctvm_demo.zip |

|
Early-Split Coding for Triangle Mesh Connectivity We describe a coder that can operate label-based similar to Edgebreaker and the Cut-Border Machine or degree-based similar to the TG coder. In either mode our coder processes vertices and triangles in the same order by performing the so-called ``split operations'' earlier than previous schemes. The main insights offered by this unified view are (a) that compression rates depend mainly on the choice of decoding strategy and less on whether labels or degrees are used and (b) how to do degree coding without storing ``split'' offsets. We also describe a new heuristic that for the first time allows the TG coder's bit-rates to drop below the vertex degree entropy. paper: is-esctmc-06.pdf slides: esctmc.ppt |
|
Streaming Compression of Triangle Meshes We radically depart from the traditional approach to mesh compression and propose a scheme that incrementally encodes a mesh in the order it is given to the compressor using only minimal memory resources. This makes the compression process basically transparent to the user and practically independent of the mesh size. This is especially beneficial for compressing large meshes where previous approaches spend significant amounts of memory, disk space, CPU time, and file I/O on pre-processing, whereas our scheme can start compressing after having been given the first few triangles. paper: ils-sctm-05.pdf slides: sctm.ppt (+vids) demo: smc_demo.zip API & source code: smc_api.zip |
|
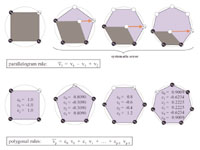
Geometry Prediction for High Degree Polygons The parallelogram rule is a simple, yet effective scheme to predict the position of a vertex from a neighboring triangle. Later, we showed that this rule is especially efficient for quad-dominant polygon meshes when applied within rather than across polygons. However, for hexagon-dominant meshes the parallelogram rule systematically performs miss-predictions. In this paper we present a generalization of the parallelogram rule to higher degree polygons. We compute a Fourier decomposition for polygons of different degrees and assume the highest frequencies to be zero for predicting missing points around the polygon. In retrospect, this theory also validates the parallelogram rule for quadrilateral surface mesh elements, as well as the Lorenzo predictor for hexahedral volume mesh elements. paper: iigs-gphdp-05.pdf slides: gphdp.ppt |
|
Lossless Compression of Predicted Floating-Point Values Scientists and engineers often refrain from using mesh compression because currently available schemes modify the mesh data. The floating-point coordinates associated with the vertices are quantized onto a uniform integer grid to enable efficient predictive compression. Although a fine enough grid can often represent the data with sufficient precision, the original floating-point values will change, regardless of grid resolution. We describe a method for compressing floating-point coordinates in a completely lossless manner. The initial quantization step is omitted and predictions are calculated in floating-point. The predicted and the actual floating-point values are broken up into sign, exponent, and mantissa and their corrections are compressed separately with context-based arithmetic coding. The achieved bit-rates nicely complement those resulting from uniformly quantizing with different precisions. papers: conference journal slides: lcfpg.ppt API & source code: lcpfpg_src.zip |
|
Streaming Meshes Today's gigabyte-sized polygon models can no longer be completely loaded into the main memory of common desktop PCs. Current mesh formats do not account for this. They were designed years ago when meshes were orders of magnitudes smaller. Using such formats to store large meshes is inefficient and unduly complicates all subsequent processing. We describe a streaming format for polygon meshes, which is simple enough to replace current mesh formats and more suitable for working with large data sets. Furthermore, it is an ideal input and output format for IO-efficient out-of-core algorithms that process meshes in a streaming, possibly pipelined, fashion. We look into both theory and practical aspects of creating and working with this new representation. We quantify qualities for streaming meshes and describe methods for converting meshes from conventional to streaming formats. paper: il-sm-05.pdf slides: sm.ppt (+vids) concept: ilgs-sfgd-05.pdf demo: sm_demo.zip API: sm_api.zip |

|
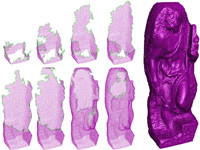
Large Mesh Simplification using Processing Sequences We show how out-of-core mesh processing techniques can be adapted to perform their computations based on the new processing sequence paradigm, which was inspired by the mesh access that our our out-of-core compressor provides during decompression, using mesh simplification as an example. A processing sequence represents a mesh as a particular interleaved ordering of indexed triangles and vertices. Only a small portion of the mesh is kept in-core, with the bulk of the mesh data residing on disk. Mesh access is restricted to a fixed traversal order, but full connectivity and geometry information is available for the active elements of the traversal. This provides seamless and highly efficient out-of-core access to very large meshes for algorithms that can adapt their computations to this fixed ordering. paper: ilgs-lmsps-03.pdf slides: lmsps.ppt (+vids) |
|
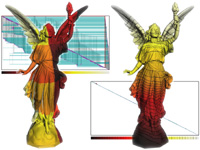
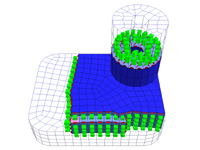
Out-of-Core Compression for Gigantic Polygon Meshes Our out-of-core mesh compression technique converts gigantic meshes into a streamable, highly compressed representation. During decompression only a small portion of the mesh needs to be in memory at any time. As full connectivity information is available along the decompression boundaries this provides seamless mesh access for incremental in-core processing on gigantic meshes. Decompression speeds are CPU-limited and exceed 1 M vertices and 2 M triangles per second on a 1.8 GHz Athlon processor. An external memory data structure provides the compressor with transparent access to large meshes. This out-of-core mesh is designed to accommodate the access pattern of our region-growing based compressor, which - in turn - performs mesh queries as seldom and as local as possible. The achieved compression rates are state-of-the-art. paper: ig-ooccgpm-03.pdf slides: oocc.ppt (+vids) demo: oocc_demo.zip lucy APIs: oocc_api.zip psreader_dist.zip psreader_dist.tar.gz |

|
A Benchmark Compressor for Polygon Meshes We offer an easily accessible online Web implementation and a downloadable standalone version of our Polygon Mesh Compressor in pure Java. This software is meant to provide benchmark bit-rates for future research in the area of mesh compression. It compresses not only the connectivity (conn) and geometry (geom) of a polygon mesh, but also one optional layer of texture coordinates. This is accomplished by compressing the texture coordinate mapping (texmap) and the texture coordinate values (texval). implements these techniques: i-cpmcddp-02.pdf ia-cpmgpp-02.pdf is-cpmpm-01.pdf is-ctcslp-03.pdf is-cpmca-02.pdf is-bcraf-03.pdf slides: cpmcddp.ppt cpmgpp.ppt cpmpm.ppt ctcslp.ppt cpmcddp.ppt cpmgpp.ppt cwa.ppt bcraf.ppt |
|
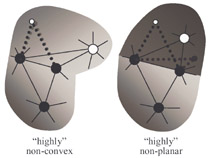
Compressing Hexahedral Volume Meshes Unstructured hexahedral volume meshes are of interest for finite element computations. When stored in a standard indexed format they take up huge amounts of space. We present the first technique for encoding connectivity and geometry of unstructured hexahedral volume meshes. For connectivity compression, we extend the idea of coding with degrees to volume meshes using edge degrees. This allows exploiting the regularity of typical hexahedral meshes. Typical compression rates are around 1.5 bits per hexahedron (bph) yet as low as 0.18 bph for highly regular meshes. The average connectivity compression ratio is 1:162. For geometry compression, we perform simple parallelogram prediction on uniformly quantized vertices within the side of a hexahedron resulting in an average geometry compression ratio of 1:3.7 at a quantization level of 16 bits. paper: ia-chvm-02.pdf demo + models: chvm_demo.zip source code: chvm_src.zip slides: chvm.ppt |
|
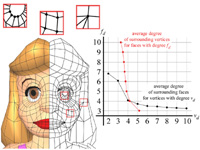
Compressing Polygon Mesh Geometry with Parallelogram Prediction We describe a simple prediction scheme for efficient compression of the vertex positions of a polygonal mesh. We provide a prototype implementation of the decoder in pure Java that proves the reported bit-rates. The 4171 vertex position of the tommygun model, for example, can be compressed to 6517 bytes. This is an improvement of 36 percent in geometry compression over the Touma-Gotsman scheme at the same quantization level of 12 bits. Our prediction scheme is not more complex than that of Touma and Gotsman ... but we do not triangulate the polygons. Instead we use the information about polygonal faces for better predictions. paper: ia-cpmgpp-02.pdf slides: cpmgpp.ppt |
|
Compressing Polygon Mesh Connectivity with Degree Duality Prediction We present a coder for polygon mesh connectivity that delivers the best connectivity compression rates meshes reported so far. Our coder is an extension of the vertex degree based coder for triangle mesh connectivity by Touma and Gotsman and borrows ideas from a paper by Alliez and Desbrun. We code polygonal connectivity as a sequence of face and vertex degrees and exploit the correlation between them for mutual predictive compression. Because low-degree vertices are likely to be surrounded by high-degree faces and vice versa, we predict vertex degrees based on neighboring face degrees and we predict face degrees based on neighboring vertex degrees. Furthermore, we provide a prototype implementation of the decoder in pure Java that proves the reported bit-rates. paper: i-cpmcddp-02.pdf slides: cpmcddp.ppt |

|
Geometry Coding for ASCII File Formats Because of the convenience of a text-based format 3D content is often published in form of a gzipped file that contains an ASCII description of the scene graph. While compressed image, audio, and video data is kept in seperate binary files, polygonal data is usually included uncompressed into the ASCII description, as there is no widely-accepted standard for compressed polygon meshes. In this paper we show how to incorporate compression of polygonal data into a purely text-based scene graph description. Our scheme codes polygon meshes as ASCII strings that compress well with standard compression schemes such as gzip. papers: is-cpmca-02.pdf is-cwa-02.pdf is-bcraf-03.pdf slides: cwa.ppt bcraf.ppt |

|
Connectivity Shapes We introduce a 3D shape representation that is based solely on mesh connectivity -- the connectivity shape. Given a connectivity, we define its natural geometry as a smooth embedding in space with uniform edge lengths and describe efficient techniques to compute it. Furthermore, we show how to generate connectivity shapes that approximate given shapes. Applications of connectivity shapes to modeling, mesh coding and graph drawing are described. paper: igg-cs-01.pdf video: cs.ram slides: cs.ppt (+vids) |
|
Face Fixer: Compressing Polygon Meshes with Properties Most schemes to compress the topology of a surface mesh have been developed for the lowest common denominator: triangulated meshes. Face Fixer was the first scheme designed to compress the topology of arbitrary polygon meshes. It encodes meshes directly in their polygonal representation and extends to capture face groupings in a natural way. Avoiding the triangulation step we reduce the storage costs for typical polygon models that have group structures and property data. paper: is-ff-00.pdf video: ff.ram demo + models + source code: ff_demo.zip slides: ff.ppt (+vids) |

|
Triangle Strip Compression We introduce a simple and efficient scheme for encoding the connectivity and the stripification of a triangle mesh. Since generating a good set of triangle strips is a hard problem, it is desirable to do this just once and store the computed strips with the triangle mesh. However, no previously reported mesh encoding scheme is designed to include triangle strip information into the compressed representation. Our algorithm encodes the stripification and the connectivity in an interwoven fashion, that exploits the correlation existing between the two. paper: i-tsc-00.pdf video: tsc.ram demo + models + source code: tsc_demo.zip slides: tsc.ppt |

|
Spirale Reversi: Reverse decoding for Edgebreaker A simple linear time algorithm for decoding Edgebreaker encoded triangle meshes in a single traversal. The Edgebreaker compression technique, introduced by Rossignac, encodes the topology of meshes homeomorphic to a sphere with a guaranteed 2 bits per triangle or less. The encoding algorithm visits every triangle of the mesh in a depth-first order. The original decoding algorithm recreates the triangles in the same order and exhibits a worst case time complexity of O(n^2). More recent work by Szymczak and Rossignac improves the worst case to O(n). However, for meshes with handles multiple traversals are needed during both encoding and decoding. We introduce here a simpler decompression technique that performs a single reverse traversal and recreates the triangles in reverse order. paper: is-sr-00.pdf slides: sr.ppt |