Table of
Contents
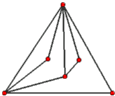
Table of
|
|
.
A pseudo-triangulation for a set P of n
points in the plane partitions the convex hull of P into
pseudo-triangles whose vertex set is exactly P, see the
Figure above for a small example. A minimum pseudo-triangulation
uses the smallest number of pseudo-triangles, which is always n-2.
Furthermore, every point set in general position also has a minimum pseudo-triangulation whose maximum face degree is four (i.e. each face of this pseudo-triangulation has at most four vertices).
The counting results are summarized in the following table. For the point set(s) with the maximal number of minimum pseudo-triangulations we give the number in the data base (table column order type # for max starting with 0 for the first set, which is in line with my tools provided below, but in contrast with Oswin Aichholzer's counting that starts with 1). The numbers are linked to the point coordinates. An example picture is available too. The last column gives access to the full binary data following the format of the order type data base.
We further observe in the data sets that the number of minimum pseudo-triangulations is always greater than the number of triangulations except if the points are in convex position where the numbers are identical. Furthermore, the points in convex position minimize the number of minimum pseudo-triangulations, which has actually now been proven to be correct for all number of points by O. Aichholzer, F. Aurenhammer, H. Krasser, and B. Speckmann in CCCG 2002, see here.
| #points | #order types | min #pseudo-tr. | max #pseudo-tr. | order type # for max | data files |
| 3 | 1 | 1 | 1 | set 0 (picture) | pseudo03.b08 |
| 4 | 2 | 2 | 3 | set 1 (picture) | pseudo04.b08 |
| 5 | 3 | 5 | 13 | set 2 (picture) | pseudo05.b08 |
| 6 | 16 | 14 | 76 | set 14 (picture) | pseudo06.b08 |
| 7 | 135 | 42 | 485 | set 124 (picture) | pseudo07.b16 |
| 8 | 3315 | 132 | 3555 | set 2990 (picture) set 3198 (picture) | pseudo08.b16 |
| 9 | 158817 | 429 | 27874 | set 151720 (picture) | pseudo09.b16 |
| 10 | 14309547 | 1430 | 234160 | set 13413893 (picture) set 13812359 (picture) | pseudo10.b32.gz |
Lutz Kettner, David Kirkpatrick, and Bettina Speckmann. Tight Degree Bounds for Pseudo-triangulations of Points. In Proc. 13th Canad. Conf. on Computational Geometry, pp. 117-120, 2001. (Abstract)
Hervé Brönnimann, Lutz Kettner, Michel Pocchiola, and Jack Snoeyink. Counting and Enumerating Pseudo-triangulations with the Greedy Flip Algorithm. In preparation. 2001. (Abstract)
Lutz Kettner. Pseudo-Triangulation Workbench (ptw): User Manual. September 2001.
The Pseudo-Triangulation Workbench (ptw) is a research tool to investigate pseudo-triangulations of points in the plane. It allows to create point sets, compute pseudo-triangulations using various algorithms, interact with them using flips, highlight interesting properties using different color schemes, and enumerate all pseudo-triangulations for a given point set. The enumeration can also be used with a branch&bound version to test hypothesis, such as minimal vertex degree. Currently, the algorithms and enumeration for pseudo-triangulations create only minimal pseudo-triangulations. Some support exists for normal triangulations, such as creation and diagonal flips. Command-line tools allow the enumeration of points sets, for example taken from the data base of order types for small point sets, without graphical user interface.
) 12.09.2001
