COMP 236 Programming Assignment 3
Write a program to display the Utah teapot as a set of parametric curves. (assignment)
Program
I implemented the program in C, using OpenGL. It is a straightforward implementation of formulas 11.28, 11.86 and 11.88-11.90 from Foley and vanDam.
To compute the points, I applied the following formulas:
![]()
![]()
![]()
where:
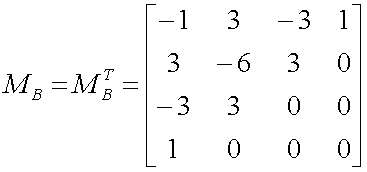 is the Bezier basis matrix.
is the Bezier basis matrix.
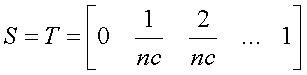 are the parameters for the parametric curves
are the parameters for the parametric curves
(nc is the number of curves, input parameter in the program, default value nc=10)
![]() are the “geometry matrices”, the Bezier control points read
from the file.
are the “geometry matrices”, the Bezier control points read
from the file.
To compute the normals, I applied the following formulas:
I computed the s tangent vector to the surface Q(s,t):
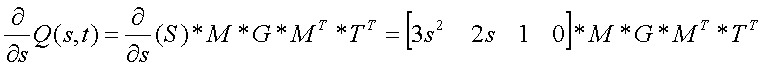
I also computed the t tangent vector to the surface Q(s,t):
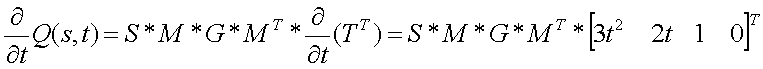
The normal vector is the cross product of the two tangent vectors:
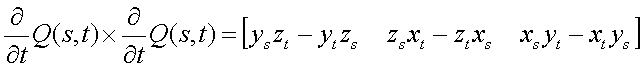
(where xs is the x component of the s tangent vector, ys is the y component of the s tangent vector, zs is the z component of the s tangent vector, etc.)
Results
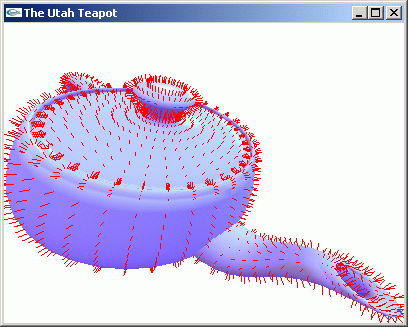
The resulting surfaces look smooth, but at the seams between the patches differences in normals make seams visible. I wrote a function that forces C1 continuity by averaging normals across common edges of pairs of patches. This took care of the large seams, but differences are still noticeable where more than two patches meet.
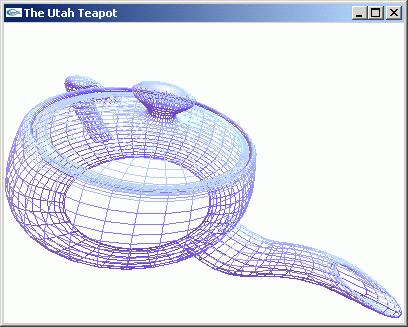
Below are a few screenshots produced by my program:
|
teapot |
teapot with normals |
|
teapot, wireframe |
teapot, wireframe with normals |
Keyboard interface
· 1,2 move the teapot in X
· 3,4 move the teapot in Y
· 5,6 move the teapot in Z
· 7,8,9,0 rotate the teapot
· w switches between normal and wireframe mode
· n switches between drawing and not drawing the normals
Links
· executable: bezier.exe
· source file: bezier.cpp
· teapot model: teapot.txt
Last modified on March 19, 2002 by Adrian Ilie.