
Write a simple ray-tracing system that will render images of clusters of spheres. (assignment)
I used Dave McAllister's approach, as he presented it in his COMP 136 lecture:
1) getting from pixels to rays:

2) Equation to describe a point P in space using its distance t along the ray:
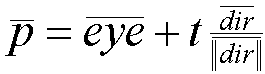
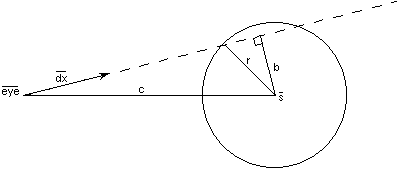
3) Computing the intersection of the ray with the sphere:
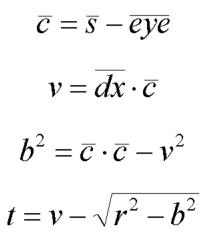
This was easier to implement with dot and cross products in C++ than the approach presented in the vanDam book. The final coode looks as follows:
bool cSphere::Intersect(const cRay&
r, cPoint& p) const
{
cVector EO(r.Origin, Center);
cVector E(cPoint(0,0,0), r.Origin); // E = vector from origin to ray origin
cVector V = r.Direction;
V = V.Normalize();
double v = V.DotProd(EO);
if (v < 0) return false;
{
double t = Radius*Radius + v*v - EO.DotProd(EO);
if (t < 0) return false;
else
{
cVector P = E + V*(v-sqrt(t));
p = P.VectorToPoint();
return true;
}
}
}
I wrote the code object-oriented, as I was planning to extend it, but I only had time to implement the first part of the assignment. I wrote classes for: points, vectors, colors, lights, rays, shapes (abstract), spheres, and tracing.
The rest of the implementation was the classic approach: generate a ray through each pixel, compute its intersection with all spheres; if an intersection is found, compute the color at the point by shooting rays from each light source.
Below are a screenshot prodced by my program and an animation generated as a succession of images:
|
A screenshot of 7spheres and 5 lights. |
|
An animation of 4 spheres, with the same lights. |
|
A screenshot of 100 spheres, with the same lights. |