COMP 236 Reading Assignment 2

Read "A Characterization of Ten Hidden-Surface Algorithms" by Sutherland, Sproull, and Shumacker. Choose one object-space method and one image-space method from the ten. Write a paper, in the form of a web page, describing how your chosen methods work. Compare and contrast your two methods with each other and with the Z-buffer (their "brute force") algorithm.

A Comparison between the Newell, Watkins and Z-buffer Algorithms

In their paper, Sutherland, Sproull and Schumacker present a classification of ten hidden‑surface algorithms. Their criterion is the space in which the solution is computed: object space vs. image space. From the algorithms presented, I chose a list‑priority algorithm and an image‑space algorithm because these are the domains in which I think further developments are more likely. Object‑space algorithms have a quadratic running time with respect to the environment complexity, so they are computationally intensive. While today’s widely‑implemented Z-buffer algorithm can also be considered computationally intensive, the elementary operations are simple enough to implement cheaply in hardware.

The Newell Hidden-Surface Algorithm

The first algorithm I chose is called a “list‑priority” algorithm because it precomputes a visibility order (called “priority”) in object‑space, then generates the picture in image‑space. This way, the algorithm takes advantage of some features of each space: priority computations are done with arbitrarily high precision in object space, yet the fact that the results are displayed on a finite‑resolution device also has a considerable impact.

As stated in the paper, the principal contributions brought about by the Newell algorithm are the “priority computer” and the concept of “overwriting” values to achieve transparency. The priority computer sorts an arbitrary collection of faces into a priority order. Transparency is achieved by allowing transparent faces that overlap other faces to overwrite their intensity values in a special way, by linear blending, if the face behind the transparent one has a higher intensity.

The algorithm consists of the following steps:

1) sort in Z: sort all the faces by depth of the furthest vertex of each face

If the faces do not overlap in Z, this sort establishes the correct priority order.

Figure 1 shows a projection of the environment on the XZ plane, so faces become lines. Sorting them in increasing Z order correctly assigns the priorities in the order F1, F2, F3.

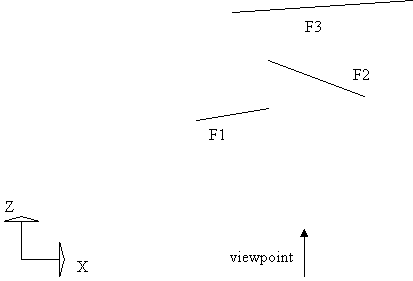
Figure 1: Sorting in Z in the Newell algorithm.

2) Newell special sort: check if the Z-order list from step 1 is in priority order, and revise if necessary

Let us consider the case in Figure 2. P is the face with the furthest vertex in Z‑order, so it is the last in the list produced in the previous step. Q is the next‑to‑last face in the same list.

If the closest vertex of P is deeper than the furthest vertex of Q, P can be safely written to the video buffer, as it does not obscure any other face. If not, we need to perform another kind of test to determine whether P obscures Q and all other faces with the furthest vertex closer than the closest vertex of P. If P obscures some face Q’ in this set, swap P and Q’ and repeat.

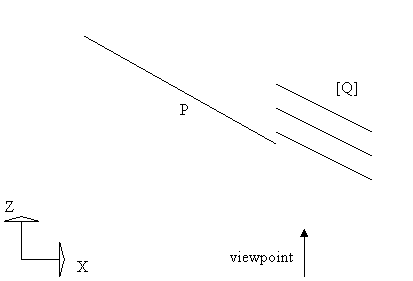
Figure 2: The Newell special sort.

To avoid infinite loops, swapped faces are marked. If a pair of unorderable faces exist, one of them must be divided into two faces to break the “cyclic overlap”, as shown in Figure 3.

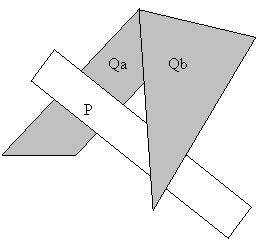
Figure 3: Breaking a cyclic overlap.

There are several tests that can be performed to check whether faces P and Q overlap. The algorithm needs to perform them in increasing order of their difficulty, until a test can decide if the two faces overlap. The tests are:

- do P and Q overlap in Z? – tested implicitly by selecting Q from the Z‑ordered list

- do the extreme X coordinates overlap? – minimax test in X

- do the extreme Y coordinates overlap? – minimax test in Y

- are all vertices of P further than the plane of Q?

- are all vertices of Q closer than the plane of P?

- do P and Q overlap on the screen?

Using these tests, a priority ordering can be decided for any environment, if appropriate breaking of cyclic overlaps are also performed.

On a final note, picture elements are not stored like in a video buffer, one for each pixel. Instead, the Newell algorithm uses “beads”, which are visible segments grouped in a “bucket” for each scan-line. This allows easy merging of new segments and overwriting values to achieve transparency.

The Watkins Hidden-Surface Algorithm

The second algorithm I chose is called an “image‑space” algorithm because it computes the answer to the hidden‑surface problem in image‑space, in a form and order suitable for a raster display. It is also called a “point‑sampling” algorithm because it samples the environment with rays that pass through infinitesimal points on the screen.

The algorithm computes the intersections of the plane of a scan-line with all the faces in the environment, resulting in segments whose coherence properties are exploited between scan-lines. Although this simplifies the hidden‑surface problem by reducing it to a two‑dimensional problem, the computed intensity of a raster element is not an average of all the contributing intensities, but a single sample point.

This results in effects like:

- objects “disappearing” between the lines, because no sample points fall within them;

- incorrect intensities at the edges of large objects because the intensity at sample points is different from the average.

These effects can be ameliorated by oversampling (in this case, situations where objects disappear can still be constructed) or random sampling (at the price of having straight edges look “fuzzy”).

The intersections of the scan-line plane with the faces in the environment define “segments”, and the scan-line is divided into “spans” within which only one segment (the closest) is visible.

As stated in the paper, the principal contributions brought about by the Watkins algorithm are the aggressive span generation and the logarithmic Z‑search. Spans are dynamic, having their left edge fixed and their right edge moved to the left as necessary when new segments are extracted from the previous list. In the logarithmic Z‑search, segments are split until the visibility can be computed with simple minimax tests, as shown in Figure 4.

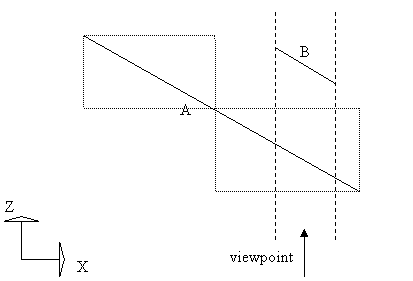
Figure 4: The Watkins logarithmic Z-search.

Here, splitting segment A in half is enough to decide that segment B is invisible.

Although this approach can ultimately lead to computing the depth of segment A at the endpoints of segment B by a large number of splits, the process usually ends much sooner.

The algorithm consists of the following steps:

1) sort in Y: limit the attention of the algorithm to the current scan-line.

This is an insertion sort: new segments are inserted in their proper place, and segments that terminate are deleted. By this incremental approach, the algorithm takes advantage of one type scan-line coherence: segments that intersect a scan-line are likely to intersect the next.

2) sort in X: examine the previous list to decide which faces are visible in which portion of the scan-line, by dividing it into spans.

3) span cull: cull out the segments within each span to determine which fall inside the span

4) Z depth search: search the segments in each span to find which one is visible.

On a final note, a hardware implementation of the Watkins algorithm was available at the time from Evans and Sutherland Computer Corporation.

The Z-buffer (“Brute Force”) Hidden-Surface Algorithm

The Z-buffer algorithm is also an “image‑space” and “point‑sampling” algorithm, so it suffers from the same drawbacks. It was developed by Catmull, and is very simple to implement. It requires, beside a frame buffer (where color values are kept), a Z-buffer (hence the name) of the same size, where a depth value is kept for each pixel.

The algorithm consists of the following steps:

0) clear the Z‑buffer.

1) “sort” in Y: limit the attention of the algorithm to the current scan-line.

2) “sort” in X: allow access the current pixel.

3) scan convert each face and “sort” in Z: for each pixel in the face’s projection, if the Z‑depth is greater than the Z‑value stored in the buffer, replace the color in the frame buffer with the face’s color at that point.

On a final note, both “sorts” in X and Y are radix sorts, so they require no comparisons. They are listed here only for comparison, since they are reduced to accessing memory locations. The “sort” in Z requires only one comparison, since it only keeps the maximum value.

Hidden-Surface Algorithm Comparison and Contrast

As shown in the paper, the computing cost for the first two algorithms is roughly the same for anisotropic environments, because they perform complex face-to-face computations only for the very few faces that overlap in all three dimensions:

- the first step in the Newell algorithm, in which faces are considered only if they overlap the depth of a test face, is just as effective as the first step in the Watkins algorithm, where faces are considered only if their vertical extent overlaps the current scan-line;

- the Newell algorithm follows the Z-depth overlap test with tests in X and Y, while the Watkins algorithm follows the Y test with overlap tests in X and Z.

In contrast, the Z-buffer algorithm needs to perform no face-to-face comparisons, the entire process being just a search over pairs {color, Z‑value}(X,Y) for fixed X and Y to find the largest Z‑value.

The first two algorithms take advantage of coherence (depth coherence in the Newell algorithm and scan-line coherence in the Warnock algorithm), while the Z‑buffer algorithm uses the brute‑force approach.

Since they are image‑space algorithms, the Watkins and Z‑buffer algorithms suffer from edge effects, while the Newell algorithm does not.