Introduction

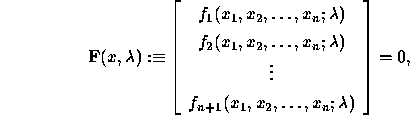
Problems of the form

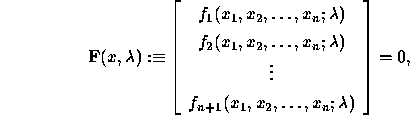
where, typically, an overconstrained system of equations is given (say 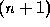equations in n unknowns), where each also depends on an additional parameter are called eigenvalue problems. This system has a solution only for specific values of . Each is an eigenvalue of the system, and the corresponding solution is the eigensolution.

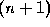We shall deal with a specific form of this problem, where all but one of the equations are linear in x and . We can formulate this problem as follows: Given a real or complex matrix , find all such that the system of equations

 ¯    ¯    ¯ = 0

		 		    		 = 1