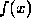 is given on the interval
is given on the interval 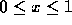 and we are asked to approximate
and we are asked to approximate 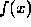 by a polynomial of degree n - 1
in x. We write the polynomial in the form
by a polynomial of degree n - 1
in x. We write the polynomial in the form



A set of matrices often used---and occasionally misused---as examples in matrix calculations is the set of Hilbert matrices. One situation in which they occur is the following:
Suppose a continuous function 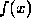 is given on the interval
is given on the interval 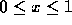 and we are asked to approximate
and we are asked to approximate 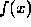 by a polynomial of degree n - 1
in x. We write the polynomial in the form
by a polynomial of degree n - 1
in x. We write the polynomial in the form

and define the error in the approximation to be
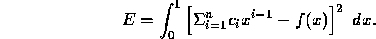
The coefficients 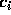 are determined by the requirement that E be
minimized. Since the error is a differentiable function of the unknowns
are determined by the requirement that E be
minimized. Since the error is a differentiable function of the unknowns 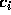 ,
at the minimum
,
at the minimum
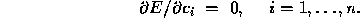
Evaluating these derivatives leads to the conditions
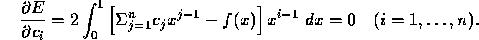
Interchanging the summation and integration, we obtain
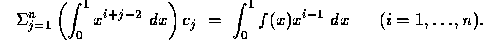
There are n equations to be satisfied by the n unknowns 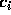 . If we let
. If we let
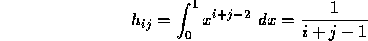
and
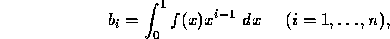
then the equations can be written as:

Thus the column of coefficients 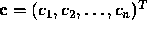 can
be found by solving the
can
be found by solving the 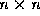 system
system

where the matrix 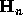 has elements
has elements
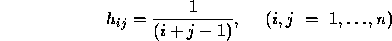
and the vector 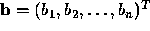 is determined by the
given function
is determined by the
given function 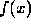 .
.
The matrix 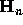 is the
is the 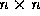 Hilbert matrix. We will let
Hilbert matrix. We will let
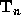 denote its inverse,
denote its inverse,

We are primarily interested in Hilbert matrices because they are very badly conditioned, even for small values of n, and because their condition number grows rapidly with n. Some of the values are shown in the table below:

The ill-conditioning nature of the Hilbert matrices can be traced back to the
approximation problem which we used to introduce them. On the interval
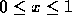 the functions
the functions 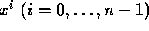 are
very nearly linearly dependent. This means that the rows of the Hilbert
matrix are very linearly dependent, i.e., that the matrix is very nearly
singular. In such cases, a small perturbations in the data can result in
large perturbations in the answers. In the original problem, small
errors in the function
are
very nearly linearly dependent. This means that the rows of the Hilbert
matrix are very linearly dependent, i.e., that the matrix is very nearly
singular. In such cases, a small perturbations in the data can result in
large perturbations in the answers. In the original problem, small
errors in the function  or rounding errors in its calculation
can result in large changes in the coefficients
or rounding errors in its calculation
can result in large changes in the coefficients 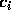 . In short, the
approximation problem is not ``well-posed" when it is in a form that
leads to a matrix like the Hilbert matrix.
. In short, the
approximation problem is not ``well-posed" when it is in a form that
leads to a matrix like the Hilbert matrix.


