|
Generalized Penetration Depth Computation and Applications to
Motion Planning 2 Publications
BackgroundPenetration depth (PD) is a distance measure to quantify the extent of inter-penetration between two overlapping, closed, geometric objects. PD computation is important in a number of applications, including physically-based modeling, robot motion planning, virtual reality, haptic rendering and computer games.
The ChallengeMost of the prior work on PD computation has been restricted to translational PD or PDt. The PDt between two overlapping objects is defined as the minimum translational distance needed to separate the two overlapping objects. Many good algorithms to estimate the PDt between convex and non-convex polyhedra are known. However, because PDt does not take into account the rotational motion, it is not sufficient for many applications, such as motion planning and physically based modeling. Highlights of our approach We take into account the translational and rotational motion to describe the extent of two intersecting objects and refer to that extent of inter-penetration as the generalized penetration depth or PDg.
Results of Generalized PD Computation
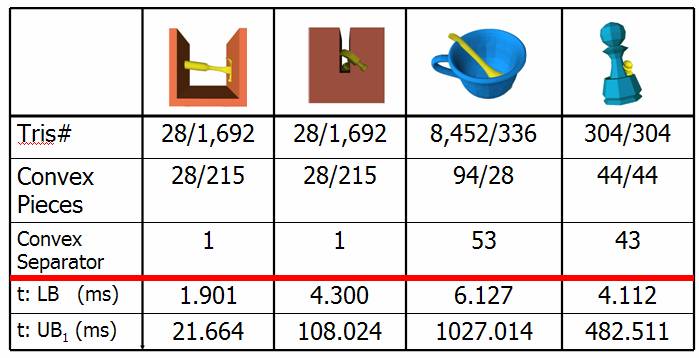
We compute an upper bound on PDg based containment optimization using linear programming.
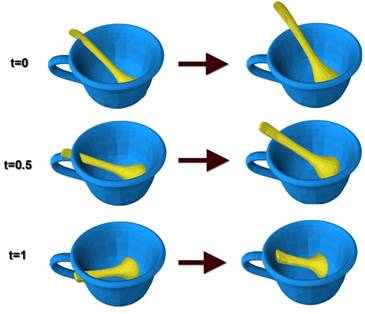
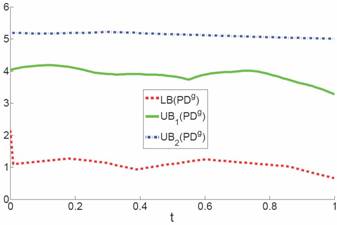
Fig. 2: In the left column, the ‘spoon’ collides with the ‘cup’ at t=0, 0.5, and 1. The right column shows for every t the corresponding collision-free configuration, which yields an upper bound on PDg. Fig. 3: The comparison of PDg computation for the ‘spoon in cup’ example. LB(PDg): Lower bound on PDg; UB1(PDg): Upper bound by our containment optimization. UB2(PDg): Trivial upper bound using the convex hulls. Tab. 1: Performance of various bounds computation on PDg Application to Motion Planning Our lower bound on PDg computation algorithm has been applied for motion planning to perform the C-obstacle query. Given a primitive in C-space, the C-obstacle query is formally defined as checking whether this primitive lies in C-obstacle space. Usually, the underlying query primitive is a cell.
In order to efficiently perform C-obstacle query for a cell, we compute the PDg by setting its configuration as the center of the cell. Then we compare it with the maximal motion that the robot can undergo when its configuration is confined within this cell. If the lower bound of PDg is larger than the upper bound of the motion, we conclude that the cell fully lies in C-obstacle space.
The C-obstacle query is useful for cell decomposition based algorithms and other complete motion planning approaches, such as star-shaped roadmap (Fig. 4). Given that the time and space complexity of these methods grows quickly with the level of subdivision, it is important to identify cells that lie in C-obstacle space and to avoid overly subdivision.
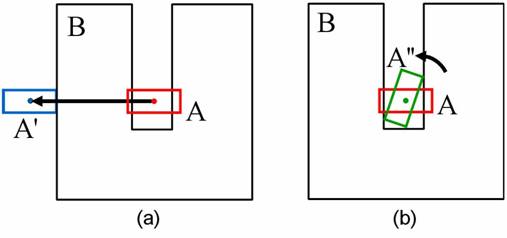
Fig. 4: An application of our C-obstacle query algorithm based on PDg for a complete motion planner – the star-shaped roadmap method. The robot Gear needs to move from initial configuration A to goal configuration A’ by translating and rotating within the shaded rectangular 2D region. We show the robot's intermediate configurations for the found path. The improved star-shaped roadmap method took about 110s for this example and achieved about 2.4 times speedup.
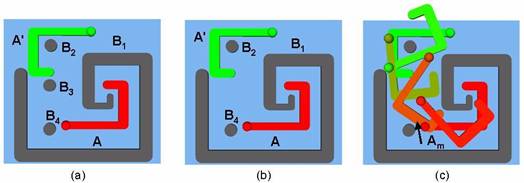
Fig. 5: ‘2D puzzle’ example. (a) Our algorithm can report the path non-existence for the problem to move A to A0 in 7.898s. (b) is a modified version of (a) without the obstacle B3. Our algorithm can find a collision-free path through a narrow passage among the obstacles. (c) shows intermediate configurations Am of the robot along the collision free path. Related Work
|