Genetic Algorithms and Character Animation

Aron Helser

Comp 291, Final Paper

Professor John Halton

May 1, 1998

  1. Introduction
  2. Driving Problem - Character Animation
    1. Physically-based Modeling
    2. Autonomous behavior
  3. Animation Solutions
    1. Alternatives to Genetic Algorithms and Autonomous Control
      1. Keyframe
      2. Other search techniques
    2. Genetic Algorithms
      1. What are GAs?
      2. Why use GAs?
      3. Results
      4. Difficulties
  4. Conclusions
    1. Emergence
  5. Future Directions for Research
    1. Burgess Shale
    2. Behavior of articulated characters
    3. Close the loop - back to keyframe
  6. References

Introduction

Character animation is a hard problem. It takes skilled animators huge amounts of time to produce an animation. Researchers have become increasingly interested in automating character animation, through the use of physically-based simulation and autonomous characters. This paper presents a review of some of this literature, focusing on the use of genetic algorithms and their application to character animation. Genetic algorithms are an optimization technique, and here they are applied to create a controller for an autonomous character. They have produced some unique results, including guided motion and unexpected means of locomotion.

Driving Problem - Character Animation

Animators spend many years becoming adept at portraying realistic motion and convincing emotion in their characters. In order to portray more realistic scenes, animators are turning to 3D animation, like that done for the feature Toy Story and many recent commercials. With increasing realism it becomes even harder to integrate character motion into a scene and to have it look plausible to a critical audience. Two ways to address this complexity are often combined: physically-based modeling and autonomous behavior.

Physically-based Modeling

Physically-based modeling provides one method for producing realistic motion in a scene. Forces we associate with the real world - gravity, contact forces, torques on joints - are simulated, along with the physical properties of the character, and the motion of the character is generated. This is a computationally intensive process, involving the solution of many equations, first to determine accelerations for all the rigid bodies in the scene and then to produce motion over a time step. Even though it is complex, it is fairly well understood, and will not be addressed further in this paper. It does generate a new problem, however: controlling the character. Forces need to be applied to the joints of a character so it will walk (or swim or jump). Generally this is encapsulated in a controller for the character. How can we design this controller?

Autonomous behavior

Once we specify the time-varying forces, the simulation will animate the character - the character's motion will be autonomous. This allows the animator to let the character go and see what happens, or to direct the overall motion without worrying about details like the motion of individual legs. The details of these options will be discussed in following sections.

In non-articulated characters, motion is often trivial - the whole character simply moves forward or turns. Instead, the character's behaviors can be specified, such as the tendency to flock, or the ability to avoid obstacles or walls [reynolds87]. This technique allows a large number of characters to be animated automatically, saving the animator a great deal of work.

Higher-level control of articulated characters is desirable for the non-expert animator. By specifying behavior, pleasing results are available to non-expert. This means many of the frequent actions for a creature must be automated. At the simplest level, the creatures must react to their environment to be realistic. They must avoid bumping into fellow creatures and other obstacles. At more complex levels, their actions are more complex, including flocking, pursuit and evasion, finding food, mating rituals, and play. Finally, traditional animators are extremely adept at giving any character human characteristics and emotions. Producing the appearance of emotion automatically is a much more difficult problem which has received only a small amount of investigation.

These aspects of animation suggest a continuum of creature control [gritz95]:

Each of these levels has been addressed to some extent in autonomous character animation, with varying degrees of success.

Animation Solutions

Alternatives to Genetic Algorithms and Autonomous Control

Keyframe

One solution is to forego physically-based modeling entirely and use keyframe animation. In this method, the animator specifies the position of the character at certain critical frames, and the character is interpolated automatically in the intervening frames (usually with splines). Keyframe animation has been the dominant form of animation in commercial software, because it comes from traditional techniques. It is still used very successfully in all kinds of animation. For instance, the film Luxo Jr. by Pixar was done entirely using keyframe animation. Keyframe animation is extremely labor intensive, so automated computer techniques have the potential to be orders of magnitude more time and labor efficient. Keyframe animation also depends heavily on the skill of the animator. Because no physical simulation is used, the animator can easily specify motion which is unappealing, because we can tell it violates physical laws somehow. Appealing animation was less difficult for the animator when the characters were largely 2D (and cartoonish), but, as 3D characters are increasingly in demand, convincing motion becomes harder to achieve. There has been work on incorporating physically-based constraints into keyframe animation. They allow the animator to choose when to use physically-based animation, so it can be disabled to allow an appealing, but non-physical, animation. Further discussion of these techniques are beyond the scope of this paper.

Keyframe animation is also impractical with a large number of characters. Animating a flock of birds would be tedious, especially if the path of the flock needed to be changed just a little to get the scene right… Automatic animation of a large number of characters is appearing in more feature films; for instance, it was used to animate bats in both Cliffhanger and Batman Returns.

Other search techniques

If we have settled on physically-based modeling, there are two routes we can take. Spacetime constraints is a technique for automatically generating character motion over the whole animation sequence at once - it optimizes in both space and time. Forward simulation methods solve time steps sequentially, using the iterative solution of differential equations for the forces and accelerations. Forward simulation relies on a controller to generate the desired joint positions of creatures.
Spacetime Constraints
In this method, a character is first constrained to a position at the beginning and ending of the simulation. Next, optionally, some intermediate positions and interactions with other characters or objects are specified. Then an objective function is specified, typically to minimize energy over the simulation, and many equations are solved spanning the whole time of the simulation. This produces a trajectory for each degree of freedom of the character. Cohen has designed a system which allows interactive direction of the optimization as it proceeds [lui94]. This gives the animator direct control over the motion of the character, while still maintaining physically-simulated realism.

This method is computationally intensive, and complex. Liu, Gortler, and Cohen [lui94] develop a wavelet basis, so the trajectories can be refined hierarchically to concentrate computational effort on areas where the trajectories change rapidly. They also use a technique from compiler design, common sub-expression elimination, to reduce the computation costs to a reasonable level. It is also notable that torques on a character's joints are never directly specified in this method - the output is a set of cubic splines specifying the change in the joint angles.

Forward methods
A more extensively investigated area is forward, step-based simulation. The objective of a character animator in these methods is the specification of a controller for a character. The controller can take several forms. In [ngo93], the controller is 10 stimulus-response pairs. The stimulus is a function of sensors in the character, and the response is a list of desired angles for all the joints in the creature. In [tu94], sensors are connected through nodes to actuators, which generate torque or force. The nodes have a binary output based on a weighted sum of their inputs. In [mckenna90], the controller is a set of coupled oscillators, with reflexive feedback, modeled on the control system of a real cockroach.

To generate an acceptable controller, we might choose to generate it by hand. Indeed, that has been the predominant way to specify controllers so far in the literature [mckenna90] [reynolds87], and some authors generate such a controller to compare with the output of their genetic algorithms [gruau95]. Hand-generating a controller is sometimes very hard, especially when the model has many degrees of freedom. Also, in some cases, hand generated controllers are inadequate. In [hodgins97], the authors adapted an existing, hand-generated controller for an adult male human running, to a female and a child. The motion achieved was awkward and robotic. This seems to have been a problem in the original controller, and it carried through into the adapted controllers. If the original controller had had more natural, organic motion, the results might have been better.

The approach many researchers have taken to generating controllers is to try to automate the process of searching for a controller. This involves trying to find an optimum solution to a large set of equations involving the parameters of the controller. There are many numerical search techniques, and many have been applied to finding controllers. The hope is that the resulting motion will be more appealing, and that these search techniques will find controllers when we are unable to hand-generate a controller. The following sections discuss how searching for a controller has worked successfully.

Stochastic Gradient Ascent
Stochastic Gradient Ascent (SGA) has been used successfully to search for locally optimal controllers for character animation [panne93]. The authors established an interesting gait by randomly generating weights for the sensor-actuator network, and then using SGA to optimize parameters which affect the quality, but not the type, of gait. Specifically, SGA perturbs a random parameter of the controller, and keeps the new controller if the character's motion gets better. A gait improved if it moved forward faster, or if the character's body had an upright posture.

SGA has a major drawback. It depends heavily on the initial guess given for the controller. If you start with a poor guess for the controller, you might not find an acceptable solution (you get stuck on a local maximum). This is true when SGA is used for spacetime constraints or forward methods. This is typical of other methods of searching for a local optimum not covered here - they depend on an initial guess being near the global optimum in order to find it.

Simulated annealing is designed to reduce this problem, by allowing the parameters to be varied randomly some of the time, thereby escaping local maxima.

Simulated Annealing
This technique is used to search for a globally optimal solution. It is similar to SGA, but uses a temperature parameter to determine the chance that a change in a parameter will be allowed to worsen the optimization. As a result, it will accept some intermediate steps which worsen the controller, while allowing the controller to get better eventually. It was also used in [panne93] to fine-tune controllers, and was found to perform competitively with SGA, converging to a solution a bit faster or slower, depending on the particular problem situation. Koza [koza94] compares simulated annealing to a genetic algorithm with a population of one. This comparison will be made more explicit later.

Both SGA and simulated annealing have some drawbacks in common. They depend on a control system model with a fixed set of parameters to optimize - in [ngo93] there are 10 stimulus-response pairs, and in [panne93] the topology of the control network is fixed: only its parameters change. The choice of these parameters is critical, and will decide whether the problem is soluble at all. The parameterizations used in these two papers are extremely rich, allowing for a wide variety of controllers. However, we can point to some results of genetic programming [sims94a] to argue that we need a controller model whose size can grow, to allow complex and organic behavior.

Finally, we would like controllers which are robust, in that they can produce similar results under varying conditions. An example might be a controller which takes a parameter indicating a target point, and hops the creature forward until it stops on that point. By taking parameters, a controller can achieve variable goals, and also adapt to changes in the environment, without running a new optimization process. The solutions arrived at by SGA and simulated annealing combined with spacetime constraints and forward methods are brittle, in that they only solve a very specific animation problem, and cannot be easily generalized. In the case of spacetime constraints, the motion is entirely specified, and a constraint, such as the end target position, cannot be modified without rerunning the entire simulation. In the forward methods, creatures are often designed just to walk/hop forward, and there is no way to have the creature stop at a specific spot, or even start moving from a different pose, perhaps from an earlier activity in an animation sequence.

Genetic Algorithms

Genetic Algorithms (GAs) are methods modeled on a natural process which provides adaptation: evolution. GAs have been used to solve the problems of producing robust controllers and globally optimal controllers found in other approaches to physically-based character animation. The next section will describe the general techniques of GAs, using examples from character animation.

What are GAs?

In GAs, a population of individuals is constructed and evaluated iteratively. Fit individuals are propagated, resulting in improved fitness in the population. After many, many generations, a solution is achieved.
Genotype and Phenotype
In humans, the genotype is contained in our DNA. A genotype is an encoding of the characteristics of an individual. These might be perceptual range, speed, strength, minimal health level to reproduce, etc., contained in a bit string of ones and zeros. In a controller, the genotype might encode the types and placements of sensors, the types of muscles, and the control connections between them. A distinction is made when the genome is of variable length, and so allows for increasing complexity as the creatures evolve. This is called genetic programming (GP), where GAs usually have genomes of fixed size. I will use the term GA to refer to both methods in this paper.

To produce an individual, its genome is evaluated; the creature that results is called the phenotype. The simulated character can then be placed in a physical simulation. In most cases investigated in the literature, the body type of the character is fixed, and the genome affects only the controller. For instance, in [ngo93] the typical creature consisted of five rigid rods, connected in different configurations. One GA optimization was performed for a Mr. Star Man character, where the rods all originated from a central point. Another featured a humanoid character, with a torso and two jointed legs. The genes of these creatures determined the parameters for 10 stimulus-response pairs; the values at which a stimulus produces a response, and the angles of the body parts which constitute a response. These genes result in motion under simulation, which along with the physical construction of the character produce its phenotype.

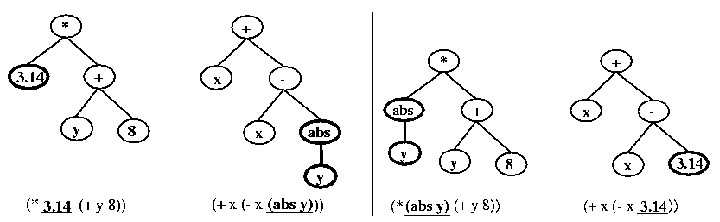
In Gritz [gritz95] [gritz97], the genotype is made up of a tree, with operators at the nodes and terminals at the leaves (see Figure 1). It uses a few simple operators, { +, -, *, %, iflte } (iflte stands for "if less than equal") and the following terminals: random floating point numbers, internal angle sensors, the position and velocity of the character, goal distance, and a goal met flag. These might combine in an expression like ( iflte ( * 0.1 px) 0.5 ( + a2 0.3 ) 0.05 ), where px and a2 are position and angle sensors. A complete expression is enclosed in parenthesis, with the operator coming first, and its operands coming next in a list. This LISP expression is evaluated by the simulator to produce a desired angle for one of the character's degrees of freedom. This evaluation, along with the character's appearance, produce the character's phenotype.

Karl Sims [sims94a] [sims94b] is unusual in that the genome in his system determines the body geometry as well as the controller, allowing for the appearance of characters to be evolved as well. This model allows for a total change in the character's appearance and behavior over time. It is not as useful for character animation, except in the generation of new design concepts.

Fitness Function
To decide whether to keep the individual's genome in the population, its fitness must be measured. This measurement can either be the result of the user's judgment, the result of an absolute function, or the result of competition with other creatures in the population.
User's Judgment
The easiest way is to let the user choose which individuals are more fit. This is appropriate when the judgment is largely esthetic, as when Karl Sims [sims91] evolved pictures using GAs. It is much too tedious when dealing with populations of thousands of individuals per generation, and hundreds of generations, as is typical of creature controllers.
Absolute
Alternatively, an absolute fitness function can be defined, like "distance traveled forward in 10 seconds". This allows automatic selection of fit individuals and allows large populations to evolve without user intervention [sims94a] [ngo93]. This is the method most often used for selecting character controllers, because the goals of character animation are often easy to define in this way. Distance traveled is an easy way to evaluate walking or swimming creatures. If a creature has the ability to sense a target, it can be evaluated by how well it follows that target, allowing for the evolution of pursuit controllers [sims94b].

Unfortunately, creatures evolved using this fitness metric are often unable to adapt to new situations, i.e., they are not robust. For instance, a creature evolved to "move forward 10 cm and stop" would be unable to "move forward 20 cm and stop." An alternative formulation uses successive fitness functions to evolve a population; once the population evolves a controller able to satisfy the first fitness function (coming within a margin of the ideal behavior), the second is introduced, and the population is evolved again to satisfy that fitness function as well. This method was used successfully in [gritz95] to evolve a controller for a Luxo lamp which hopped forward and stopped at different places. In [gruau95], a neural net controller was evolved that was able to achieve 6 legged tripod motion from any starting position of the six legs. This method is used because the GA often will not find any useful solutions if the initial fitness function is too hard to satisfy, similar to simulated annealing.

Competition
Some tasks are naturally competitive in nature. Individuals in the population can be pitted against each other, and their fitness measured relative to each other [reynolds94b] [sims94b]. This method is has been used for simulating biologically realistic creatures in artificial life research, because it mirrors competition with other creatures and interaction with the environment in natural settings. It is also useful when an absolute fitness function is hard to specify, but the winner(s) of a competition can be determined. The method for selecting opponent creatures while minimizing the number of contests has been investigated by several researchers. Methods from all-vs.-all competition, to tournaments, to random competition with another individual have been used [reynolds94b].
Evolution
How is fitness used to improve the population's performance overall? A genetic algorithm tries to exploit the good characteristics of fit individuals, while still maintaining genetic diversity so that it can explore different solutions. Generally, the fitness of the individual affects the probability of its genome continuing into the next generation. Even poor individuals have some chance of continuing, and fit individuals have some chance of being eliminated, so that the population continues to vary and explore many possibilities in an attempt to provide good coverage of the search space. There is wide variation in the methods used to select the individuals that go on to the next generation, and GAs do not seem particularly sensitive to which is used [koza94].

Once fit individuals are selected, their genes must be propagated. This can be done by mutation or sexual reproduction.

Mutations
The genes of a successful individual can be copied, and a few random changes can be added to its genes. The type of change is adapted to the genome - nodes can be added or deleted, mathematical functions can be switched, or constants altered. Often some of the mutations are designed to have small effects, like the modification of a constant by a small amount, while others allow for dramatic changes, like the insertion of a new node into the controller.

Koza [koza94], in a general discussion of genetic programming, points out that mutation is used very sparingly in many applications, and that sexual crossover is the biggest source of diversity and useful genetic material. In fact, in the examples in his book, mutation is not used at all.

Sexual
Alternatively, the genes of two individuals can be combined sexually. If the genomes are of the same length, then the gene for each position can be chosen randomly from the parents' genotypes. If the genome is of variable length, "crossover" is often used (see Figure 1). If crossover is chosen as a means of propagation, nodes are chosen in each of the parents' genomes, and the balanced sub-trees at those nodes are exchanged. This allows successful subparts of the controller to stay together, while still producing new (and hopefully interesting) controllers. Other methods of sexual reproduction can be used, especially on the directed graphs used in [sims94a], but they are similar in spirit to crossover.

Figure 1. This illustrates crossover on an expression tree, and was taken from [gritz95]. On the left are the parents, with the selected cross-over nodes in bold. On the right are the resulting children.

All Together
The final result is a population of individuals which are evaluated during each generation; some are eliminated, and the remainder are combined into a new generation. Then the process repeats for hundreds or thousands of generations. The typical individual's fitness will improve, until the rate of improvement tapers off or the population's performance meets the termination criteria. The most successful controllers are chosen from the final generation. Often the controllers can have very different structures, and solve the same problem in very different ways. Sometimes it is necessary to perform several runs to get different controllers, because a particular genome can come to dominate the population, as discuss in the Problems section.

Why use GAs?

They work. GAs have been applied to many different types of problems, and have proved to be a very successful global optimization technique. In character animation, researchers have obtained some fun and startling results, discussed in the next section. But why do they work?
Global search technique
One reason GAs work is that they are a global search technique. The initial population takes a random sample of the search space, usually limited to relatively simple controllers. Mutation and sexual cross-over ensure that more complex controllers are explored as well, often in widely different parts of the search space. The search is also guided by human creativity, through the choice of fitness functions to produce more interesting and acceptable results.

GAs have been used to attack and solve a remarkable variety of problems. The subjects in a recent GA proceedings include NP complete problems, pattern recognition, shop flow, control strategies, aircraft design, stack filters, and Steiner trees.

Koza [koza94] has two explanations why GAs using sexual reproduction are so successful. The fitness function can be thought of as defining a terrain, and a controller is placed on this terrain according to its fitness. Then it wanders around trying to find the top of the highest mountain in the terrain (the optimal solution). Wandering is implemented by replacing the controller with a new one, or with many new ones, for GAs. In simulated annealing and SGA, there is only one controller wandering this fitness terrain. With SGA, it is constrained to travel uphill only. If it started near a small hill, it gets stuck and can't find the mountain. With simulated annealing, it can travel downhill, but if it is far away from the mountain, it will have a hard time finding the mountain. In genetic algorithms with mutation, there are hundreds or thousands of controllers searching the terrain, having their positions changed a little or a lot by mutation. Those that find a hill will be replicated so that the uphill area is searched more thoroughly. This may cost much more in computational time than simulated annealing, but because there are more controllers searching, it may find the highest mountain much faster.

When we add sexual crossover to the mix, the situation becomes more complicated. If two individuals are crossed, we can picture a new individual arriving on the fitness plane somewhere between the two parents. It's hard to say what the terrain will be under this new individual. But if both the parents were judged fit, then they are on a rise in the terrain. There could be a valley between them, but more likely there is more high terrain, maybe even the mountain we are looking for. Of course, this analogy simplifies the problem considerably, because, if the genome has 12 parameters, the terrain has 12 dimensions. If the genome has a variable structure, the terrain has potentially infinite dimensions. Koza explains this property in terms of schema. A schema is a set of genes, with some of the positions in the genotype filled with a "don't care" terminal. This represents a set of individuals which share the same genes, except where the "don't care" symbol appears in the schema. When we pick a cross-over site in an individual, we are defining a schema with a "don't care" symbol at that site. The individual serves as a sample of all the individuals that share that schema. Since the individual is fit, hopefully the schema is fit, too. When we intersect two fit schemata, we are more likely to find fit individuals. Schemata and their relationship to choosing fit individuals has been investigated in the theoretical literature of GAs [koza94].

Huge search space
It is very hard to specify torques around joints so that a character behaves the way the animator wants. Torque is not a natural way for an animator to specify the motion of a figure. The number of degrees of freedom of an articulated character grows very rapidly with its complexity, and it becomes correspondingly harder to specify its controls. Even with simple two or three link characters, GAs have found some motions which were not anticipated by the authors [ngo93].

With GAs, the search space does not have to be limited. GAs can combine the sensors, internal nodes and effectors in a control system in arbitrary ways, to allow controllers of very different forms than might be designed by hand.

The use of a variable fitness function also allows for the design of robust controllers. Gritz [gritz95] [gritz97] uses a function which starts with a main goal (reach point X at the end of the time allotment) and gradually adds in additional style points, for completing the motion early and staying put, penalties for falling over or hitting its head. This allows the main goal to evolve individuals which are then refined by the style restrictions. Additionally, fitness was averaged over multiple tries with different end-target points, resulting in controllers which could move any distance and stop. The lamp had learned the skill of moving forward and stopping, instead of learning the action of "move forward 30 cm." This may be successful with SGA or simulated annealing as well, but has not been investigated in the literature so far.

Behavior
Biological Simulation and experimentation
One of the things we have come to expect from the natural world is complexity. Even in simple activities like walking, there is variation in the individual and wide variation between individuals as to how it is accomplished. GAs allow a controller to increase in complexity, and so allow for behaviors which are complex, and meet our expectations for subtle variation and organic appearance in motion [gritz97].

If effort is made to model creatures on aspects of biology, researchers hope that GAs can be used to study the motion, behavior and evolution of real creatures. In [gruau95], a controller was based on a biological model of a cockroach's neural system. Interestingly, the GA produced a controller which, compared to a hand designed controller, was more robust, in that it could start from any leg position, and used fewer nodes.

Results

Motions
Here are some examples of unique motions evolved by a GA. In [ngo93], the 2D articulated figures evolve shuffling forward motion, as well as a leap followed by a roll, and a cartwheel. These may be thought of as an idea generator - these characters are not seen in nature, so their motions are not easily visualized. The GA searches for controllers that allow the creature to cover the greatest distance, thereby synthesizing unique motions.

In [gritz95], expression tree controllers described in the Genotype and Phenotype section are evolved. First, two controllers for a Luxo-style lamp are investigated. One of them uses a progressive fitness function to allow the lamp to hop forward and stop on a spot 10 to 60 cm in front of it. In the second, the lamp learns to duck under a horizontal pole by the introduction of a penalty in the fitness function for hitting the pole. Controllers for a human model are also evolved, for controlling from 6-10 degrees of freedom of a 28 degrees of freedom model. The model learns to touch an object in space, and touch its nose. These results show how control of an animated character can be carefully directed by the animator, even though the details of the motion are generated automatically by the GA.

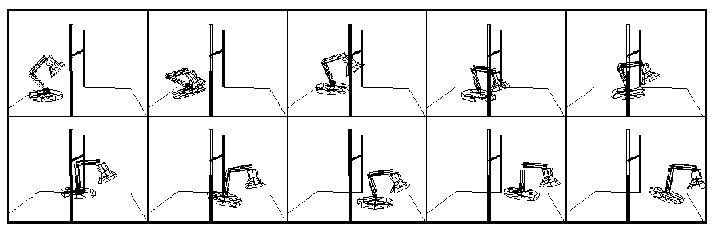
Figure 2. This is taken from [gritz95], and shows the behavior of the Luxo lamp avoiding an overhead bar as it hops.

[gruau95] shows another robust controller. The controller produces 6-legged tripod motion, in which three legs are down and three legs move forward at any time. The evolved controller is able to start from any initial leg positions, where the hand-designed controller made by the authors is not able to do this. Craig Reynolds has also investigated generating robust controllers through the introduction of noise in sensor input and effector output [reynolds94a], as discussed in the Problems sections.

There are also some recent results which show that GAs are not the only way to go. In [tu94], random weights are generated for the sensor-actuator network controllers, and then SGA is used to tune other parameters in the controllers, so as to maintain the basic gait. They find some robust controllers for a 4 legged hopper which allow it to navigate up a small incline, though the optimization process took place on flat terrain. However, the authors note that their technique was not able to find interesting controllers for more complex creatures, of six or more links.

Unique creatures
GAs also allow some unique experimentation. Karl Sims [sims94a] [sims94b] allowed the shape of his creatures to evolve, along with their controllers. The creature structure was defined with a directed graph, which allowed widely varied solutions to walking motion, from long snakes, to walking and hopping motions, to creatures that wave an appendage in the air to hop their body forward. His creatures evolved for swimming include some phenotypes similar to those in nature - snake-like creatures, those with two paddles and a tail, or a body and four paddles. But they also include creatures with huge paddling appendages, segmented bodies with 2 paddles each, and wildly asymmetrical bodies with three appendages.

The animator would probably use a tool like this as an idea generator. The simplified model of creature construction allows shapes and behaviors not found in nature to evolve readily.

Difficulties

Non-understandable controller
It is often very difficult to understand why the controllers produced through GAs work the way they do. Many times this understanding is not necessary, because the controller is simply used and the creature's behavior observed. But a change in behavior then cannot be implemented through simply modifying the controller (although this would be non-trivial even with a hand-designed controller). Instead, the creature(s) must be evolved further to adapt to the new behavior.
Optimality and stability
Because predicting the behavior of a controller is extremely difficult, it is usually not possible to say anything about its stability, except through repeated observation. Craig Reynolds [reynolds94b] has been studying stability and optimality. In a simple game of tag, the optimal controller is known: if you are It, directly chase the other player. If you are not It, run directly away from the pursuer. He found that GAs evolved controllers which performed surprisingly close to the optimal behavior, even though they did not appear to match the optimal response pattern. He has also found [reynolds94a] that noise can be introduced in the readings of sensors and the outputs of actuators to make controllers less dependent on the specifics of the fitness trials - i.e., more robust. Some (but not all) of the controllers he evolved to navigate a specific corridor were able to navigate through novel corridors, like some that changed width or had 60-degree instead of 90-degree turns.
Convergence to useful solutions not assured
Finally, GAs often do not converge to useful results without some tweaking. In [ngo93], the controller for a bipedal figure was evaluated on the basis of the forward motion of the center of mass. The population of controllers converged very quickly to the strategy of falling forwards, and was unable to evolve any more interesting strategies. When the evaluation metric was changed to the forward motion of the point between the figure's feet, the GA produced more interesting walking/hopping motions.

In this way GAs are similar to other numerical techniques. SGA is designed only to find a local optimum, and simulated annealing was designed to address this shortcoming. Because of their large populations and variety of genetic material available for solution of the problem, GAs are more suited for global optimization than SGA. But because they are probabilistic, results from two otherwise identical runs can be quite different, and we are not guaranteed to find a solution, where SGA will at least find a locally optimal solution. Premature convergence is a condition in GAs where a mediocre solution comes to dominate the population in early generations, and because the population lacks a variety of genetic material, it cannot break away from the mediocre, locally optimal, solution and find a better one. Often this problem can be solved by adjusting the fitness function, or simply by re-running the simulation.

Gritz [gritz97] showed one way to deal with this problem, by starting the population with an easier fitness function and gradually adding style restrictions. An alternative that does not use GAs is presented by van de Panne [panne95]. The authors introduce a "hand of God" torque to keep the character upright, and then uses a simple gradient ascent optimization to have the character learn to walk. Then the influence of the stabilizing torque is reduced and eliminated in two more stages of optimization. Both of these approaches change the shape of the fitness landscape, making it easier to get near a solution to start, and then specializing towards the final, desired controller.

Conclusions

The research presented in this paper about autonomous character animation is just a start. These results show that GAs can be used to produce robust controllers that follow the animator's directions, or idea-generating motions that were not expected by the animator. Other search techniques have been and continue to be used successfully to design controllers for character animation, but the characteristics of GAs make them better for finding complex, organic controllers. GAs may also be useful for simulating biological behavior. Finally, GAs can exhibit another property: emergence.

Emergence

This is a theme that appears again and again in the artificial life literature, and has been recognized in character animation since Reynolds wrote about flocks and boids [reynolds87]. Groups of creatures with local views of their environments, and acting based on that local knowledge, can exhibit surprising global behavior, such as the coordinated motion of flocks. The term has been generalized to refer to startling behavior encountered in other situations, such as that in GAs. The large population provides a fertile ground for unexpected behaviors, built up from simple controller components which don't exhibit any startling behavior in isolation.

Future Directions for Research

Burgess Shale

Animators now have many controllers for realistic models of creatures in a physically-based modeling setting. An example is the hand-designed controller for an insect, modeled on a simplified cockroach [mckenna90]. The cyclic controllers for the legs are modeled on those postulated in real insects, and the control system is fairly robust. Similarly, [tu94] created a practical but greatly simplified model of fish and their swimming muscles, along with a behavior-based controller. Creatures with GA evolved controllers should allow more complex and realistic models from biology than have been previously explored.

One place where this might prove particularly useful is in the study of the Burgess Shale [gould90]. This is a fossil record of animal life just before a mass extinction. There are many body types totally unrelated to those that have survived to the modern day. It would be fascinating to evolve controllers for these bodies, because we have no living examples to give us any idea about how these creatures might have moved or behaved.

Behavior of articulated characters

There has been considerable work in designing realistic behavior for autonomous characters. One notable example is [tu94], in which the authors design a simplified skeleton and muscular structure for a fish, and then hand designed controllers which allow the fish to move forward, and turn left and right. These basic skills are then linked into a behavior controller, which allows the fish to pursue such goals as find food, escape predators, school, court and mate. In [grzeszczuk95], the authors showed the results of allowing simulated annealing to design separate controllers for swimming forward, and left and right, and then synthesizing them. However, only a small amount of work has been done with evolving higher-level behaviors of creatures like this, and GAs have not yet been applied.

Craig Reynolds has also investigated deterministic, reactive controllers based on local information, which give creatures the appearance of intention. His model of flocks [reynolds87] is a purely reactive model based on the local environment of the bird, but it gives the overall flock the appearance of intention and global coordination. He has also evolved robust, reactive controllers for simple vehicles with sensors which follow a corridor [reynolds94a]. Even though these are reactive actions, they can be used by an animator to give a character what appears to be proactive behavior.

In [tu94] and [grzeszczuk95], higher level behaviors are synthesized from lower level skills. Skills like walking forward and stopping have been successfully designed by GAs, so behaviors are a logical and challenging next goal. Possible strategies include simply continuing to evolve the controller for a skill, so that it exhibits more complex behavior, or freezing the skill controllers and using them as basic building blocks in a controller for a behavior. As computational capabilities increase, this kind of design becomes more feasible.

Close the loop - back to keyframe

Since keyframe animation still dominates commercial tools, it would be useful to integrate autonomous characters into keyframe systems. Once we have the physically-based motion of a creature and its controller, especially one that has evolved skills like "move forward and stop", we should be able to integrate the creature into a keyframe system so that its motions are portrayed in real-time to the animator. This might mean extracting the physical simulation portion, since this is the most computationally intensive, and replacing it with a kinematic description. However, a controller that can chase a target or stop after a varying distance may be impossible to describe kinematically.

References

[gould90] S. J. Gould. Wonderful Life : The Burgess Shale and the Nature of History. W W Norton & Co. 1990.

[gritz97] l. Gritz, J. K. Hahn. Genetic Programming Evolution of Controllers for 3-D Character Animation. Koza, J.R., et al. (editors), Genetic Programming 1997: Proceedings of the 2nd Annual Conference, 139-146, July 13-16 1997, Stanford University. San Francisco: Morgan Kaufmann. 1997.

[gritz95] l. Gritz, J. K. Hahn. Genetic Programming for Articulated Figure Motion. Journal of Visualization and Computer Animation, vol. 6, no. 3, pp. 129-142, July 1995.

[gruau95] F. Gruau. Modular Genetic Neural Networks for 6-Legged Locomotion. J.M. Alliot, et al. [editors], Artifical Evolution '95, (AE95), pages 201-219. Springer. 1995.

[grzeszczuk95] R. Grzeszczuk, D. Terzopoulos. Automated Learning of Muscle-Actuated Locomotion Through Control Abstraction, ACM Computer Graphics, Proceedings of SIGGRAPH'95, August 1995.

[hodgins97] J. Hodgins, N. Pollard. Adapting Simulated Behavior For New Characters. In SIGGRAPH 97 Conf. Proc., pages 153-162, Los Angeles, California, August 1997.

[koza94] J. R. Koza. Genetic Programming 2: Automatic Discovery of Reusable Programs. Cambridge, MA: MIT Press. 1994.

[liu94] Z. Liu, S. J. Gortler, M. F. Cohen. Hierarchical spacetime control. In SIGGRAPH 94 Conf. Proc., pages 35-42, Orlando, Florida, July 1994.

[mckenna90] M. McKenna, D. Zeltzer. Dynamic Simulation of Autonomous Agents. In Computer Graphics, 24(4), August 1990, pages 29-38.

[michel95] O. Michel. An Artificial Life Approach for the Synthesis of Autonomous Agents. In Artifical Evolution '95, (AE95), J.M. Alliot, et al., Editors, Springer, 1995, pages 220-231.

[ngo93] J. T. Ngo and J. Marks. Spacetime constraints revisited. In SIGGRAPH 93 Conf. Proc., pages 343-350, Anaheim, California, Aug. 1993.

[reynolds94a] C. W. Reynolds. Evolution of Corridor Following Behavior in a Noisy World. In From Animals to Animats 3: Proceedings of the Third International Conference on Simulation of Adaptive Behavior (SAB94), D. Cliff, P. Husbands, J-A Meyer, and S. Wilson, Editors, ISBN 0-262-53122-4, MIT Press, Cambridge, Massachusetts, 1994, pages 402-410.

[reynolds94b] C. W. Reynolds. Competition, Coevolution and the Game of Tag. In Artificial Life IV, R. Brooks and P. Maes, Editors, ISBN 0-262-52190-3, MIT Press, Cambridge, Massachusetts, 1994, pages 59-69.

[reynolds87] C. W. Reynolds. Flocks, Herds, and Schools: A Distributed Behavioral Model, in Computer Graphics, 21(4) (SIGGRAPH '87 Conference Proceedings), pages 25-34.

[sims91] K. Sims. Artificial evolution for computer graphics. In Computer Graphics (SIGGRAPH 91 Conf. Proc.), volume 25, pages 319-328, Las Vegas, Nevada, July 1991.

[sims94a] K. Sims. Evolving virtual creatures. In SIGGRAPH 94 Conf. Proc., pages 15-22, Orlando, Florida, July 1994.

[sims94b] K. Sims. Evolving 3D Morphology and Behavior by Competition. In Artificial Life IV Proceedings, ed. by R. Brooks & P. Maes, MIT Press, 1994, pages 28-39.

[tu94] X. Tu and D. Terzopoulos. Artificial Fishes: Physics, Locomotion, Perception, Behavior. In SIGGRAPH 9 Conf. Proc., Orlando, Florida, July 1994, July 1994.

[panne93] M. van de Panne and E. Fiume. Sensor-actuator networks. In SIGGRAPH 93 Conf. Proc., pages 335-342, Anaheim, California, Aug. 1993.

[panne95] M. Van de Panne and A. Lamouret. Guided Optimization for Balanced Locomotion, in Computer Animation and Simulation '95, 165-177, Sept 2-3 1995, Maastricht, the Netherlands: Springer-Verlag/Wien. 1995.

References which look interesting but I don't have.

[]Koza, John R. 1992. Genetic Programming: On the Programming of Computers by Means of Natural Selection. Cambridge, MA: MIT Press.

[] J. Ventrella. Disney meets Darwin - the evolution of funny animated figures. In Proc. of Computer Animation 95, pages 35-43, Apr. 1995.

[] A. Witkin and M. Kass. Spacetime constraints. In Computer Graphics (SIGGRAPH 88 Conf. Proc.), volume 22, pages 159-168, Atlanta, Georgia, Aug. 1988.

[]Reynolds, C. W. (1988) Not Bumping Into Things, in the notes for the SIGGRAPH '88 course Developments in Physically-Based Modeling, pages G1-G13, published by ACM SIGGRAPH.

[]Reynolds, C. W. (1993) An Evolved, Vision-Based Behavioral Model of Coordinated Group Motion, in From Animals to Animats 2: Proceedings of the Second International Conference on Simulation of Adaptive Behavior (SAB92), Meyer, Roitblat and Wilson editors, ISBN 0-262-63149-0, MIT Press, Cambridge, Massachusetts, pages 384-392.

[]Reynolds, C. W. (1994) An Evolved, Vision-Based Model of Obstacle Avoidance Behavior, in Artificial Life III, Santa Fe Institute Studies in the Sciences of Complexity, Proceedings Volume XVI, C. Langton, Editor, ISBN 0-201-62494-X, Addison-Wesley, Redwood City, California, pages 327-346.

[]Reynolds, C. W. (1994) Evolution of Obstacle Avoidance Behavior: Using Noise to Promote Robust Solutions, in Advances in Genetic Programming, K. E. Kinnear, Jr., Ed., ISBN 0-262-11188-8, MIT Press, Cambridge, Massachusetts, pages 221-242.

[]Reynolds, C. W. (1994) The Difficulty of Roving Eyes, in Computational Intelligence: Imitating Life (Proceedings of the 1994 IEEE World Congress on Computational Intelligence) Orlando, Florida, USA, June 27-29, ISBN 0-7803-1104-3, IEEE Press, pages 262-267.