Character animation is a hard problem. It takes skilled animators huge amounts of time to produce an animation. Researchers have become increasingly interested in automating character animation, through the use of physically-based simulation and autonomous characters. This paper presents a review of some of this literature, focusing on the use of genetic algorithms and their application to character animation. Genetic algorithms are part of a class of optimization techniques, and here they are applied to create a controller for an autonomous character. They have produced some unique results, including guided motion, and unexpected means of locomotion.
Animators spend many years becoming adept at portraying realistic motion and convincing emotion in their characters. In order to portray more realistic scenes, animators are turning to 3D animation, like that done for the feature Toy Story and many recent commercials. With increasing realism it becomes even harder to integrate character motion into a scene and to have it look plausible to a critical audience. Two ways to address this complexity are often combined; physically-based modeling and autonomous behavior.
Physically-based modeling provides one method for producing realistic motion in a scene. Forces we associate with the real world - gravity, contact forces, torques on joints - are simulated, along with the physical properties of the character, and the motion of the character is generated. This is a computationally intensive process, involving the solution of many equations first to determine accelerations for all the rigid bodies in the scene, and then to produce motion over a time step. Even though it is complex, it is fairly well understood, and will not be addressed further in this paper. It does generate a new problem, however: controlling the character. Torques need to be applied to the joints of a character so it will walk (or swim or jump). Generally this is encapsulated in a controller for the character. How can we design this controller?
Once we specify the time-varying torques, the character will animate itself - it will be autonomous. This allows the animator to either let the character go and see what happens, or direct the overall motion without worrying about details like the motion of individual legs. I'm not specifying exactly how this is done, because the details come later.
In non-articulated characters, behavior and motion become somewhat ambiguous. The character's motions tend to define behaviors: tendency to flock, or the ability to avoid obstacles or walls [reynolds87] .
Interesting interaction with other creatures can include flocking behavior and competitive abilities. The creatures also must react to their environment to be realistic. At the simplest level, they must avoid bumping into obstacles and fellow creatures. At more complex levels, they can pursue higher level goals including pursuit and evasion, finding food, mating rituals and play.
Cel animators are extremely adept at portraying their
characters with human characteristics and emotions. Producing
the appearance of emotion automatically is a much more difficult
problem which has received only a small amount of investigation.
These goals of animation suggest a continuum of creature control [gritz95]:
Beyond these might be emotional responses and complex character interaction. Each of these levels has been addressed to some extent in autonomous character animation, with varying degrees of success.
One solution is to forego physically-based modeling entirely and use keyframe animation. In this method, the animator specifies the position of the character at certain critical frames, and the character is interpolated automatically in the intervening frames (usually with splines). Keyframe animation has been the dominant form of animation in commercial software, because it comes from traditional techniques. It is still used very successfully in all kinds of animation. For instance, the film Luxo Jr. by Pixar was done entirely using keyframe animation. Keyframe animation is extremely labor intensive, so automated computer techniques have the potential to be orders of magnitude more time and labor efficient. Keyframe animation also depends heavily on the skill of the animator. Because no physical simulation is used, the animator can easily specify motion which is unappealing, because we can tell it violates physical laws somehow. This was less difficult for the animator when the characters were largely 2D (and cartoonish), but as 3D characters are increasingly in demand, convincing motion becomes harder to achieve. There has been work on incorporating physically-based constraints into keyframe animation, but those techniques are beyond the scope of this paper.
This type of keyframe animation is also impractical with a large number of characters. Animating a flock of birds would be tedious, especially if the path of the flock needed to be changed just a little to get this scene right… Automatic animation of a large number of characters is appearing in more feature films; for instance, it was used to animate bats in both Cliffhanger and Batman Returns.
If we have settled on physically-based modeling, we have two routes we can take. Spacetime constraints is a technique for automatically generating character motion over the whole animation sequence at once - it optimizes in both space and time. Forward simulation methods solve time steps sequentially, using the iterative solution of differential equations for the forces and accelerations. Forward simulation relies on a controller to create the motion of creatures.
In this method, a character is first constrained to a position at the beginning and ending of the simulation, as well as some intermediate positions, and interactions with other characters or objects. Then an objective function is specified, typically to minimize energy over the simulation. Then many equations are solved spanning the whole time of the simulation, and a trajectory for each degree of freedom (DOF) of the character is produced. For instance, a character with three joints would have the angle of each of its joints produced as a set of three cubic splines. Cohen has designed a system which allows interactive direction of the optimization as it proceeds [lui94]. This gives the animator direct control over the motion of the character, while still maintaining physically-simulated realism.
This method is computationally intensive, and complex. Liu, Gortler, and Cohen [lui94] develop a wavelet basis so the trajectories can be refined hierarchically and concentrate computational effort on areas where the trajectories change rapidly. They also use a technique from compiler design, common sub-expression elimination, to reduce the computation costs to a reasonable level. It is also notable that torques on a character's joints are never directly specified in this method - the output is a set of functions specifying the change in the joint angles.
A more extensively investigated area is forward, step-based simulation. The objective of a character animator in these methods is the specification of a controller for a character. The controller can take several forms. In [ngo93], the controller is 10 stimulus response pairs. The stimulus is a function of sensors in the character, and the response is a list of desired angles for all the joints in the creature. In [tu94], sensors are connect through nodes to actuators, which generate torque or force. The nodes have a binary output based on a weighted sum of their inputs. In [mckenna90], the controller is a set of coupled oscillators, with reflexive feedback, modeled on the control system of a real cockroach.
To generate an acceptable controller, we might choose to generate it by hand. Indeed, that has been the predominant way to specify controllers so far in the literature [mckenna90][reynolds87], and some authors generate such a controller to compare with the output of their genetic algorithms [gruau95]. Hand-generating a controller is sometimes very hard, especially when the model has many DOF. Also, in some cases, hand generated controllers are inadequate. In [hodgins97], the authors adapt an existing, hand-generated controller for an adult male human running to a female and a child. The motion achieved was awkward and robotic. This seemed to be a problem in the original controller, and it carried through into the adapted controllers. If the original controller had more natural, organic motion, the results might have been better received.
The approach many researchers have taken to generating controllers is to try and automate the process by searching for a controller. This involves trying to find an optimum solution to a large set of equations involving the parameters of the controller. There are many numerical search techniques, and many have been applied to finding controllers. The hope is that the resulting motion will be more appealing, and that these search techniques will be able to find controllers where we are unable to hand generate a controller.
Stochastic Gradient Ascent (SGA) has been used successfully to search for locally optimal controllers for character animation [panne93]. It perturbs a random parameter of the controller, and keeps the new controller if it gets better. The authors established an interesting gait by randomly generating weights for the sensor-actuator network, and then use SGA to optimize parameters which affect the quality, but not the type, of gait. In this way they were able to tune the gait to be more stable and move faster.
This technique is used to search for a globally optimal solution. It is similar to SGA, but uses a temperature parameter to determine the chance that a change in a parameter will be allowed to worsen the optimization. As a result, it will accept some intermediate steps which worsen the controller, but forces the controller to get better eventually. It was also used in [panne93] to fine-tune controllers, and was found to perform competitively with SGA, converging to a solution a bit faster or slower depending on the particular problem situation. Koza [koza94] compares simulated annealing to a genetic algorithm with a population of one.
Both SGA and simulated annealing have some drawbacks in common. Each of these methods depend on the initial guess given for the controller. If you start with a poor guess for the controller, you might not find an acceptable solution (you get stuck on a local maximum). This is true for spacetime constraints as well as the forward methods, although simulated annealing is designed to minimize this problem. This is typical of other methods of searching not covered here - they depend on an initial guess being near the global optimum in order to find it.
They also depend on a fixed set of parameters to optimize - in [ngo93] there are 10 stimulus-response pairs, and in [panne93] the topology of the control network is fixed, only its parameters change. The choice of these parameters is critical, and will decide whether the problem is solvable at all. The parameterizations used in these two papers are extremely rich, allowing for a wide variety of controllers. However, we can point to some results of genetic programming to argue that we need a controller which is not fixed in size, to allow the development of complexity and organic behavior in the controller.
Finally, the solutions arrived at by all of these methods are brittle, in that they only solve a very specific animation problem, and cannot be easily generalized. In the case of spacetime constraints, the motion is entirely specified, and a constraint, such as the end target position, cannot be modified without rerunning the entire simulation. In the forward methods, creatures are often designed just to walk/hop forward, and there is no way to have the creature stop at a specific spot, or even start moving from a different position, perhaps from an earlier activity in an animation sequence. We would like controllers which are robust, in that they can start from different positions and take parameters to adjust their motion, while still remaining largely automatic in their operation. In this way they can achieve variable goals, and also adapt to changes in their environment, without running a new optimization process.
Genetic Algorithms (GAs) are methods that use one of nature's most powerful search techniques: evolution. GAs can be used to solve many of the problems in other approaches to physically-based character animation. The next section will describe the general techniques of GAs, using examples from character animation.
GAs are based on Darwinian "survival of the fittest". A population of individuals is constructed, and evaluated iteratively. Fit individuals are propagated, resulting in improved fitness in the population. After several generations, a solution is achieved.
In humans, the genotype is contained in our DNA. In GAs, the simplest form of genotype is a bit string of ones and zeros, encoding the characteristics of an individual. These might be things like perceptual range, speed, strength, minimal health level to reproduce, etc. In a controller, the genotype might encode the types and placements of sensors, the types of muscles, and the control connections between them. These formulations often resemble lisp expressions. A distinction is made when the genome is variable in length, and so allows for increasing complexity as the creatures evolve. This is called genetic programming (GP), where GAs usually have genomes of fixed size. I will use the term GA to refer to both methods in this paper.
To produce an individual character, its genome is evaluated, to make the simulated character. It can then be placed in a physical simulation. In most cases investigated so far, the body type of the character is fixed, and the genome only affects the controller. For instance, in [ngo93], the typical creature consisted of five rigid rods, connected in different configurations. One GA run was performed for a Mr. Star Man character, where the rods all originated from a central point. Another featured a humanoid character, with a torso and two legs. The genes of these creatures determine the parameters for 10 stimulus-response pairs; the values at which a stimulus produces a response, and the angles of the body parts which constitutes a response. These genes result in motion under simulation, which along with the physical construction of the character produce its phenotype.
In Gritz [gritz95][gritz97], the genotype is made up of a LISP S-expression. It uses a few simple operator, { +, -, *, %, iflte } and the following terminals: random floating point numbers, internal angle sensors, the position and velocity of the character, goal distance, and a goal met flag. These might combine in an expression like ( iflte ( * 0.1 px) 0.5 ( + a2 0.3 ) 0.05 ), where px and a2 are position and angle sensors. This lisp expression is evaluated by the simulator to produce a desired angle for one of the character's DOF. This evaluation, along with the character's appearance, produce the character's phenotype.
Karl Sims [sims94a][sims94b] is unusual in that the genome determines the body geometry as well as the controller, allowing for the appearance of characters to be evolved as well. This model is closest to what we think occurs in nature, because it allows for a total change in the character's appearance and behavior over time. For the same reason, it is not as useful for character animation, except in the generation of new ideas.
To decide whether to keep the individual's genome in the population, its fitness must be measured. There are several methods for doing so, described below.
The easiest way is to let the user choose which individual is fit. This is appropriate when the judgment is largely esthetic, as when Karl Sims [sims91] evolved pictures with GAs. It is much too tedious when dealing with populations of thousands of individuals per generation, as is typical of creature controllers.
Alternately, an absolute fitness function can be defined, like "distance traveled forward in 10 seconds". This allows automatic selection of fit individuals and allows large populations to evolve rapidly [sims94a][ngo93]. This is the method most often used for selecting character controllers, because the goals of character animation are often easy to define in this way. Distance traveled is an easy way to evaluate walking or swimming creatures. If a creature has the ability to sense a target, it can be evaluated on how well it follows that target, allowing for evolution of pursuit controllers [sims94b].
Unfortunately, creatures evolved using this fitness metric often unable to adapt to new situations. For instance, a creature evolved to "move forward 10 cm and stop" would be unable to "move forward 20 cm and stop." An alternative formulation uses successive fitness functions to evolve a population; once the population evolves a controller able to satisfy the first fitness function (coming within a margin of the ideal behavior), the second is introduced, and the population is evolved again to satisfy that fitness function as well. This method was used successfully in [gritz95] to evolve a controller for a Luxo lamp which hopped forward and stopped at different places. In [gruau95], a neural net controller was evolved that was able to achieve 6 legged tripod motion from any starting position of the six legs.
Some tasks are naturally competitive in nature, like a game of tag. Then individuals in the population can be pitted against each other, and their fitness measured relative to each other [reynolds94b][sims94b]. This method is the most useful for simulating biologically realistic creatures, because the only measure of fitness in nature is the evaluation of how well a creature survives in competition with other creatures and interaction with the environment. This method is used very often in artificial life research. The method for selecting opponent creatures while minimizing the number of contests has been investigated by several researchers. Methods from all-vs.-all competition, to tournaments, to random competition with another individual have been used [reynolds94b].
How does fitness get used to improve the population's performance overall? Unfit individuals should be eliminated, and the good characteristics of fit individuals propagated into the population. Most often, the fitness of the individual affects the probability of its genome continuing into the next generation. Even poor individuals have a chance of continuing, and fit individuals have a small chance of being eliminated, so that the population stays varied and explores many possibilities - i.e. good coverage of the search space. There is wide variation in the methods used to select the individuals that go on to the next generation, and GAs do not seem particularly sensitive to which is used.
Once fit individuals are selected, their genes must be propagated.
One can just copy the genes of a successful individual, and sometimes make a random change to the genes. The type of change is adapted to the genome - nodes can be added or deleted, and mathematical functions can be switched, or constants altered. Often some of the mutations are designed to have small effects, like the modification of a constant by a small amount, while others allow for dramatic changes, like the insertion of a new node into the controller.
Koza [koza94], in a general discussion of GP, points out that mutation is often used very sparingly in many applications, and that sexual crossover is the biggest source of diversity and useful genetic material. In fact, in the examples in his book, mutation is not used at all.
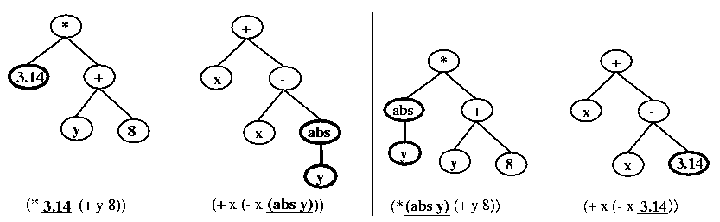
Alternately, the genes of two individuals can be combined sexually. If the genomes are the same length, then the gene for a position can be chosen randomly from one parent. If the genome is variable length, "crossover" is often used. If crossover is chosen as a means of reproduction, two individuals are chosen from the population, as explained above. Nodes are chosen in each of the parent's genomes, and the balanced sub-trees at those nodes are exchanged. This allows successful subparts of the controller to stay together, while still producing new (and hopefully interesting) controllers. Other methods of sexual reproduction can be used, especially on the directed graphs used in [sims94a], but they are similar in spirit to crossover.

This figure illustrates crossover on an expression tree, and was taken from [gritz95]. On the left are the parents, with the selected cross-over nodes in bold. On the right are the resulting children.
The final result is a population of individuals which are evaluated during each generation, some are eliminated, and the remainder are combined into a new generation. Then the process repeats for hundreds or thousands of generations. The typical individual's fitness will improve, until the rate of improvement tapers off or the population's performance meets the termination criteria. Then the GA returns the most successful controller or controllers. Often they can have very different controllers, and solve the problems in very different ways. Sometimes it is necessary to perform several runs to get different controllers, because a particular genome can come to dominate the population, as discuss in the Problems section.
First and foremost, because they work. GAs have been applied to many different types of problems, and have proved to be a very successful global optimization technique. In character animation, researchers have obtained some fun and startling results, discussed in the next section. But why do GAs work?
One reason is that GAs are a global search technique. The initial population takes a random sample of the search space, usually limited to relatively simple controllers. But mutation and sexual cross-over insure that more complex controllers are explored as well, often in widely different parts of the search space. Human creativity comes into play, in tweaking the fitness function to produce more interesting and acceptable results.
GAs have been used to attack and solve a remarkable variety of problems. The subjects in a recent GA proceedings include NP complete problems, pattern recognition, shop flow, control strategies, aircraft design, stack filters, and Steiner trees.
Koza [koza94] has two explanations why GAs using sexual reproduction are so successful. The fitness function can be thought of as defining a terrain, and a controller is placed on this terrain based on its fitness. Then it wanders around trying to find the top of the highest mountain in this terrain (the optimal solution). In simulated annealing and SGA, there is only one controller wandering this fitness terrain. With SGA, he is constrained to only travel uphill. If he started near a small hill, he gets stuck and can't find the mountain. With simulated annealing, he can travel downhill, but if he is far away from the mountain, he will have a hard time finding it. In genetic algorithms with mutation, there are hundreds or thousands of controllers searching the terrain, having their positions changed a little or a lot by mutation. Ones that find a hill will be replicated so that the uphill area is searched more thoroughly. This may cost more in computational time than simulated annealing, but because there are more controllers searching, it may find the highest mountain much faster.
When we add sexual crossover to the mix, the situation becomes more complicated. If two individuals are crossed, we can picture a new individual arriving on the fitness plane somewhere between the two parents. It's hard to say what the terrain will be under this new individual. But if both the parents were judged fit, then they are on a rise in the terrain. There could be a valley between them, but more likely there is more high terrain, maybe even the mountain we are looking for. Of course, this analogy simplifies the problem considerably, because if the genome has 12 parameters, the terrain has 12 dimensions. If the genome has a variable structure, the terrain has potentially infinite dimensions. Koza explains this property in terms of schema. A schema is a set of genes, with some of the positions in the genotype filled with a "don't care" terminal. This represents a set of individuals which share the same genes, except where the "don't care" symbol appears in the schema. When we pick a cross-over site in an individual, we are defining a schema with a "don't care" symbol at that sight. The individual serves as an estimate of all the individuals that share that schema. Since the individual is fit, hopefully the schema is fit, too. And when we intersect two fit schemata, we are more likely to find fit individuals. Schemata and their relationship to choosing fit individuals has been investigated in the theoretical literature of GAs [koza94].
It is very hard to specify torques around joints so that a character behaves the way the animator wants. Torque is not a natural way for an animator to specify the motion of a figure. And the number of DOF of an articulated character grows very rapidly with its complexity, and it becomes correspondingly harder to specify its controls. Even with simple two or three link characters, GAs have found some motions which were not anticipated by the authors [ngo93].
With GAs, the search space does not have to be limited. GAs can combine the sensors, internal nodes and effectors in a control system in arbitrary ways, to allow controllers of very different forms than might be designed by hand.
The use of a variable fitness function also allows for the design of robust controllers. Gritz [gritz95][gritz97] uses a function which starts with a main goal (reach point X at the end of the time allotment) and gradually adds in additional style points, for completing the motion early and staying put, penalties for falling over or hitting its head. This allows the main goal to evolve individuals which are then refined by the style restrictions. Additionally, fitness was averaged over multiple tries with different end-target points, which resulted in controllers which could move any distance and stop. The lamp had learned the skill of moving forward and stopping, instead of learning the action of "move forward 30 cm."
One of the things we have come to expect from the natural world is complexity. Even in simple activities like walking, there is variation in the individual and wide variation between individuals as to how it is accomplished. GAs allow a controller to increase in complexity, and so allow for behaviors which are complex, and meet our expectations for subtle variation and organic appearance in motion [gritz97].
GAs are related, indirectly, to the natural process of evolution. If effort is made to model creatures on aspects of biology, researchers hope that GAs can be used to study the motion, behavior and evolution of real creatures. In [gruau95], a controller was designed based on a biological model of a cockroach's neural system. Interestingly, the GA produced a controller which was more robust, in that it could start from any leg position, and used fewer nodes than the hand designed controller.
Here are some examples of unique motions evolved by a GA. In [ngo93], the 2D articulated figures evolve shuffling forward motion, as well as a leap followed by a roll, and a cartwheel. These may be thought of as an idea generator - these characters are not seen in nature, so their motions are not easily visualized. The GA searches for controllers that allow the creature to cover the greatest distance, the thereby synthesizes unique motions.
In [gritz95], two controllers for a Luxo-style lamp are evolved. One of them uses a progressive fitness function to allow the lamp to hop forward and stop on a spot from between 10 to 60 cm in front of it. In the second, the lamp learns to duck under a horizontal pole by the introduction of a penalty in the fitness function for hitting the pole. Controllers for a human model are also evolved, for controlling from 6-10 DOF of a 28 DOF model. The model learns to touch an object in space, and touch its nose. These results show how control of an animated character can be carefully directed by the animator, yet the details of the motion are generated automatically by the GA.
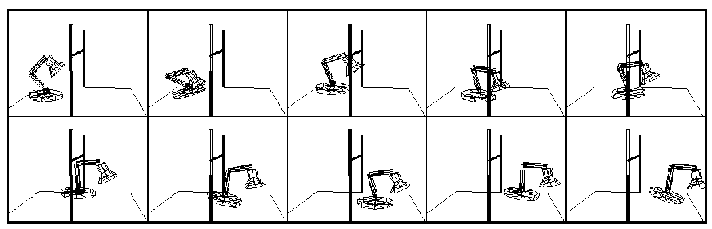
This figure is taken from [gritz95], and shows the behavior of the Luxo lamp avoiding an overhead bar as it hops.
[gruau95] shows another robust controller. The controller produces 6-legged tripod motion, in which three legs are down and three legs move forward at any time. The evolved controller is able to start from any initial leg positions, where the hand-designed controller made by the authors is not able to do this. Craig Reynolds has also investigated generating robust controllers through the introduction of noise in sensor input, and effector output [reynolds94a], as discussed in the Problems sections.
There are also some recent results which show that GAs are not the only way to go. In [tu94], random weights are generated for the sensor-actuator network controllers, and then SGA is used to tune other parameters in the controllers, so as to maintain the basic gait. They find some robust controllers for a 4 legged hopper which allow it to navigate up a small incline, while the optimization process took place on flat terrain. However, the authors note that their technique was not able to find interesting controllers for more complex creatures, of six or more links.
GAs also allow some unique experimentation. Karl Sims [sims94a][sims94b] allowed the shape of his creatures to evolve, along with their controllers. The creature structure was defined with a directed graph, which allowed widely varied solutions to walking motion, from long snakes, to walking and hopping motions, to creatures that wave an appendage in the air to hop their body forward. His creatures evolved for swimming include some phenotypes similar to those in nature - snake-like creatures, those with two paddles and a tail, or a body and four paddles. But they also include creatures with huge paddling appendages, segmented bodies with 2 paddles each, and wildly asymmetrical bodies with three appendages.
The animator would probably use a tool like this as an idea generator. Because of the simplified model of creature construction, strange and asymmetric creatures evolve. These creature solve problems in novel ways.
One problem with GAs is also an advantage. It is often impossible to understand why the controllers produced through evolution work the way they do. Many times this understanding is not necessary, because the controller is simply used and the creature's behavior observed. But a change in behavior then cannot be implemented through simply modifying the controller (although this would be non-trivial even with a hand-designed controller). Instead, the creature(s) must be evolved further to adapt to the new behavior.
Along the same vein, because predicting the behavior of a controller is extremely difficult, it is usually not possible to say anything about the stability of a controller except through repeated observation. Craig Reynolds [reynolds94b] has been studying stability and optimality. In a simple game of tag, the optimal controller is known: if you are It, directly chase the other player. If you are not It, run directly away from the pursuer. He found that GAs evolved controllers which performed surprising close to the optimal behavior, even though they did not appear to match the optimal response pattern. He has also found [reynolds94a] that noise can be introduced in the readings of sensor and the output of actuators to make controllers less dependent on the specifics of the fitness trials - i.e. more robust. Some (but not all) of the controllers he evolved were able to navigate through novel corridors, like ones that changed width or had 60 instead of 90 degree turns.
Finally, GAs often do not converge to useful results without some tweaking. In [ngo93], the controller for a bipedal figure was evaluated based on the forward motion of the center of mass. The population of controllers converge very quickly on the strategy of falling forwards, and was unable to evolve any more interesting strategies. When the evaluation metric was changed to the forward motion of the point between the figure's feet, the GA produced more interesting walking/hopping motions.
In this way GAs are similar to other numerical techniques. SGA is designed to only find a local optimum, and simulated annealing was designed to address this shortcoming. Because of their large populations and variety of genetic material available for solution of the problem, GAs are more suited for global optimization than SGA and simulated annealing. But because they are probabilistic, results from two otherwise identical runs can be quite different, and we are not guaranteed to find a solution, where SGA will at least find a locally optimal solution. Premature convergence is a condition in GAs where a mediocre solution comes to dominate the population early in the run, and because of the population lacks a variety of genetic material, it cannot break away from the mediocre, locally optimal solution, and find a better one. Often this problem can be solved by adjusting the fitness function, or simply re-running the simulation.
Gritz [gritz97] showed one way to deal with this problem, by starting the population with an easier fitness function and gradually adding style restrictions. An alternative that does not use GAs is presented by van de Panne [panne95]. The authors introduce a "hand of God" torque to keep the character upright, and then uses a simple gradient ascent optimization to have the character learn to walk. Then the influence of the stabilizing torque is reduced and eliminated in two more stages of optimization. Both of these approaches change the shape of the fitness landscape, making it easier to get near a solution to start, and then specializing towards the final, desired controller.
The research presented in this paper about autonomous character animation is just the beginning. These results show that GAs can be used to produce robust controllers that follow the animator's directions, or idea-generating motions that were not expected by the animator. Other search techniques have been and continue to be used successfully to design controllers for character animation, but the characteristics of GAs make them better for finding complex, organic controllers. GAs may also be useful for simulating biological behavior. Finally, GAs can exhibit another property: emergence.
This is a theme that appears again and again in the artificial life literature, and has been recognized in character animation since Reynolds wrote about flocks and boids [reynolds87]. Groups of creatures with local views of their environments, and acting based on that local knowledge, can exhibit surprising global behavior, such as the coordinated motion of flocks. The term has been generalized to refer to startling behavior encountered in other situations, such as that in GAs. The large population provides a fertile ground for unexpected behaviors, built up from simple controller components which don't have any startling behavior in isolation.
Animators now have many controllers for realistic models of creatures in a physically-based modeling setting. An example [mckenna90] is the hand-designed controller for an insect, modeled on a simplified cockroach. The cyclic controllers for the legs are modeled on those postulated in real insects, and the control system is fairly robust. Similarly, [tu94] created a practical but greatly simplified model of fish and their swimming muscles, along with a behavior-based controller. Creatures with GA evolved controllers should allow more complex and realistic models from biology than have been previously explored.
One place where this might prove particularly useful is in the study of the Burgess Shale [gould90]. This is a fossil record of animal life just before a mass extinction. There are many body types totally unrelated to those that have survived to the modern day. It would be fascinating to evolve controllers for these bodies, because we have no living examples to give us any idea about how these creatures might have moved or behaved.
There has been considerable work in designing realistic behavior for autonomous characters. One notable example is [tu94], in which the authors design a simplified skeleton and muscular structure for a fish, and then hand designed controllers which allow the fish to move forward, and turn left and right. These basic skills are then linked into a behavior controller, which allows the fish to pursue such goals as find food, escape predators, schooling, courting and mating. In [grzeszczuk95], the authors showed the results of allowing simulated annealing to design separate controllers for swimming forward, left and right, and then synthesizing them. However, only a small amount of work has been done with evolving higher-level behaviors of creatures like this.
Craig Reynolds has also investigated reflexive action which appears to be behavior. His model of flocks [reynolds87] is a purely reactive model based on the local environment of the bird, but it gives the overall flock the appearance of intention and global coordination. He has also evolved robust, reactive controllers for simple vehicles with sensors which follow a corridor [reynolds94a]. Even though these are reactive actions, they can be used by an animator to give a character with what appears to be proactive behavior.
In [tu94] and [grzeszczuk95] , higher level behaviors are synthesized from lower level skills. Skills like walking forward and stopping have been successfully designed by GAs, so behaviors are a logical and challenging next goal. Possible strategies include simply continuing to evolve the controller for a skill so that it exhibits more complex behavior, or freezing the skill controllers and using them as basic building blocks in a controller for a behavior. As computational capabilities increase, this kind of design becomes more feasible.
Since keyframe animation still dominates commercial tools, it would be useful to integrate autonomous characters into keyframe systems. Once we have the physically-based motion of a creature and its controller, especially one that has evolved skills like "move forward and stop", we should be able to integrate the creature into a keyframe system such that its motions are portrayed in real-time to the animator. This might mean extracting the physical simulation portion, since this is the most computationally intensive, and replacing it with a kinematic description. The problem is to maintain any parameterization which has been included in the controller in this kinematic description.
[gould90] S. J. Gould. Wonderful Life : The Burgess
Shale and the Nature of History. W W Norton & Co. 1990.
[gritz97] l. Gritz, J. K. Hahn. Genetic Programming
Evolution of Controllers for 3-D Character Animation. Koza, J.R.,
et al. (editors), Genetic Programming 1997: Proceedings of
the 2nd Annual Conference, 139-146, July 13-16 1997, Stanford
University. San Francisco: Morgan Kaufmann. 1997.
[gritz95] l. Gritz, J. K. Hahn. Genetic Programming
for Articulated Figure Motion. Journal of Visualization and
Computer Animation, vol. 6, no. 3, pp. 129-142, July 1995.
[gruau95] F. Gruau. Modular Genetic Neural Networks
for 6-Legged Locomotion. J.M. Alliot, et al. [editors], Artifical
Evolution '95, (AE95), pages 201-219. Springer. 1995.
[grzeszczuk95] R. Grzeszczuk, D. Terzopoulos. Automated
Learning of Muscle-Actuated Locomotion Through Control Abstraction,
ACM Computer Graphics, Proceedings of SIGGRAPH'95, August
1995.
[hodgins97] J. Hodgins, N. Pollard. Adapting Simulated
Behavior For New Characters. In SIGGRAPH 97 Conf. Proc.,
pages 153-162, Los Angeles, California, August 1997.
[koza94] J. R. Koza. Genetic Programming 2: Automatic
Discovery of Reusable Programs. Cambridge, MA: MIT Press.
1994.
[liu94] Z. Liu, S. J. Gortler, M. F. Cohen. Hierarchical
spacetime control. In SIGGRAPH 94 Conf. Proc., pages 35-42,
Orlando, Florida, July 1994.
[mckenna90] M. McKenna, D. Zeltzer. Dynamic Simulation
of Autonomous Agents. In Computer Graphics, 24(4), August
1990, pages 29-38.
[michel95] O. Michel. An Artificial Life Approach
for the Synthesis of Autonomous Agents. In Artifical Evolution
'95, (AE95), J.M. Alliot, et al., Editors, Springer, 1995,
pages 220-231.
[ngo93] J. T. Ngo and J. Marks. Spacetime constraints
revisited. In SIGGRAPH 93 Conf. Proc., pages 343-350, Anaheim,
California, Aug. 1993.
[reynolds94a] C. W. Reynolds. Evolution of Corridor
Following Behavior in a Noisy World. In From Animals to
Animats 3: Proceedings of the Third International Conference on
Simulation of Adaptive Behavior (SAB94), D. Cliff, P. Husbands,
J-A Meyer, and S. Wilson, Editors, ISBN 0-262-53122-4, MIT Press,
Cambridge, Massachusetts, 1994, pages 402-410.
[reynolds94b] C. W. Reynolds. Competition, Coevolution
and the Game of Tag. In Artificial Life IV, R. Brooks and
P. Maes, Editors, ISBN 0-262-52190-3, MIT Press, Cambridge, Massachusetts,
1994, pages 59-69.
[reynolds87] C. W. Reynolds. Flocks, Herds, and Schools:
A Distributed Behavioral Model, in Computer Graphics, 21(4)
(SIGGRAPH '87 Conference Proceedings), pages 25-34.
[sims91] K. Sims. Artificial evolution for computer
graphics. In Computer Graphics (SIGGRAPH 91 Conf. Proc.),
volume 25, pages 319-328, Las Vegas, Nevada, July 1991.
[sims94a] K. Sims. Evolving virtual creatures. In
SIGGRAPH 94 Conf. Proc., pages 15-22, Orlando, Florida,
July 1994.
[sims94b] K. Sims. Evolving 3D Morphology and Behavior
by Competition. In Artificial Life IV Proceedings, ed.
by R. Brooks & P. Maes, MIT Press, 1994, pages 28-39.
[tu94] X. Tu and D. Terzopoulos. Artificial Fishes:
Physics, Locomotion, Perception, Behavior. In SIGGRAPH 9 Conf.
Proc., Orlando, Florida, July 1994, July 1994.
[panne93] M. van de Panne and E. Fiume. Sensor-actuator
networks. In SIGGRAPH 93 Conf. Proc., pages 335-342, Anaheim,
California, Aug. 1993.
[panne95] M. Van de Panne and A. Lamouret. Guided
Optimization for Balanced Locomotion, in Computer Animation
and Simulation '95, 165-177, Sept 2-3 1995, Maastricht, the
Netherlands: Springer-Verlag/Wien. 1995.
References not included in the paper, but which look interesting.
[]Koza, John R. 1992. Genetic Programming: On the
Programming of Computers by Means of Natural Selection. Cambridge,
MA: MIT Press.
[] J. Ventrella. Disney meets Darwin - the evolution
of funny animated figures. In Proc. of Computer Animation 95,
pages 35-43, Apr. 1995.
[] A. Witkin and M. Kass. Spacetime constraints.
In Computer Graphics (SIGGRAPH 88 Conf. Proc.), volume
22, pages 159-168, Atlanta, Georgia, Aug. 1988.
[]Reynolds, C. W. (1988) Not Bumping Into Things,
in the notes for the SIGGRAPH '88 course Developments in Physically-Based
Modeling, pages G1-G13, published by ACM SIGGRAPH.
[]Reynolds, C. W. (1993) An Evolved, Vision-Based
Behavioral Model of Coordinated Group Motion, in From Animals
to Animats 2: Proceedings of the Second International Conference
on Simulation of Adaptive Behavior (SAB92), Meyer, Roitblat and
Wilson editors, ISBN 0-262-63149-0, MIT Press, Cambridge, Massachusetts,
pages 384-392.
[]Reynolds, C. W. (1994) An Evolved, Vision-Based
Model of Obstacle Avoidance Behavior, in Artificial Life III,
Santa Fe Institute Studies in the Sciences of Complexity, Proceedings
Volume XVI, C. Langton, Editor, ISBN 0-201-62494-X, Addison-Wesley,
Redwood City, California, pages 327-346.
[]Reynolds, C. W. (1994) Evolution of Obstacle Avoidance
Behavior: Using Noise to Promote Robust Solutions, in Advances
in Genetic Programming, K. E. Kinnear, Jr., Ed., ISBN 0-262-11188-8,
MIT Press, Cambridge, Massachusetts, pages 221-242.
[]Reynolds, C. W. (1994) The Difficulty of Roving
Eyes, in Computational Intelligence: Imitating Life (Proceedings
of the 1994 IEEE World Congress on Computational Intelligence)
Orlando, Florida, USA, June 27-29, ISBN 0-7803-1104-3, IEEE Press,
pages 262-267.