Computing Visibility Without Depth
Leonard McMillan
A fundamental problem in computer graphics is the determination of the visible subset of surface elements within a scene given the desired viewpoint. Often, the best method for computing visibility is depends on the form and properties of the scene's description. This paper presents a visibility algorithm for a specific type of scene description, called a perspective-projected surface. Surfaces of this type are commonplace, since they describe nearly all physically-based image-formation processes. The algorithm establishes a particular drawing order where the last surface drawn at any image region corresponds to the visible surface in that region, similar to the classic painter's algorithm. The unique aspect of the algorithm is that the drawing order is established independent of the scene's geometry- in particular the depth values relative to the viewing surface. The paper goes on to give a formal proof of the algorithm's correctness.
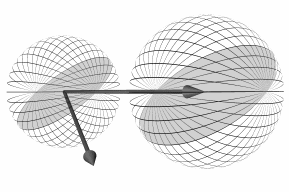
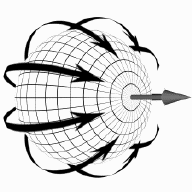
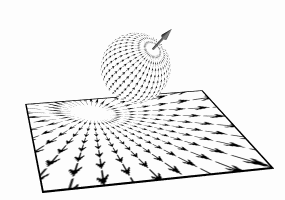
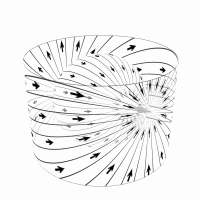
Figure 1. All perspective-projected surfaces can be mapped onto a spherical manifold. Any subsequent re-projection of that surface to a manifold with a different center of projection induces an unique coordinate frame for the original surface. In this induced coordinate system an occlusion compatable ordering for performing the reprojection can be established independent of the underlying range function.


Figure 2. A selection of images from the paper that demonstrate the algorithm's application to various projection manifolds.