Connectivity Shapes
Martin Isenburg Stefan Gumhold Craig Gotsman

abstract:
In this paper we introduce a 3D shape representation that is based solely
on mesh connectivity -- the connectivity shape. Given a
connectivity, we define its natural geometry as a smooth
embedding in space with uniform edge lengths and describe efficient techniques
to compute it. Furthermore, we show how to generate connectivity
shapes that approximate given shapes. Applications of connectivity
shapes to modeling, mesh coding and graph drawing are described.
publication:
[igg-cs-01.pdf] Martin Isenburg, Stefan Gumhold, Craig Gotsman, Connectivity Shapes, Proceedings of Visualization 2001, pages 135-142, October 2001.
download:
video: cs.ram
slides: cs.ppt (+ embedded videos)
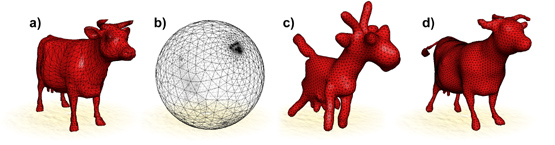
In the Figure above we see the well-known polygonal mesh of a cow (a).
Ignoring the geometry, we have mapped the cow's connectivity onto the
unit sphere (b), where the different densities hint to the features of
the cow. In (c) the corresponding connectivity shape is shown.
It is a smooth embedding with uniform edge lengths of the connectivity
graph of (a) and (b) in three dimensional space.
Imagine all edges of the cow being springs of the same equilibrium
length. In the embedding (b) we forced the spring system into
a high energy state. In (c) we released all vertices and the spring
system relaxed into a low energy state, with more or less uniform
edge lengths. This is the connectivity's natural shape. More poetically, the
sphere embedding in (b) has the body of a sphere, but the soul
of an animal. The natural embedding in (c) reveals the geometric soul
of the cow's connectivity.
We can also to generate connectivity shapes that
approximate given shapes. This is done by (re)meshing the given
shape with uniform edge lengths. For example, the connectivity
shape in (d) bears a striking resemblance to the original (a).
The only information in this mesh is its connectivity, in the
sense that it induces the mesh geometry.
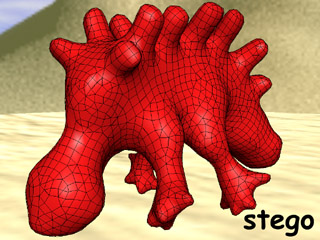
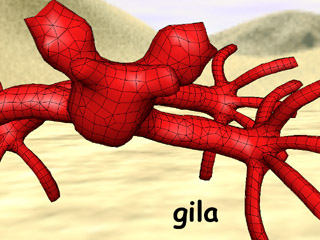
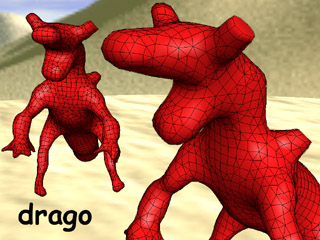
Connectivity Creatures: