Early-Split Coding for Triangle Mesh Connectivity
Martin Isenburg Jack Snoeyink
abstract:
The two main schemes for coding triangle mesh connectivity traverse a mesh
with similar region-growing operations. Rossignac's
Edgebreaker uses triangle labels to encode the traversal whereas the coder
of Touma and Gotsman uses vertex degrees.
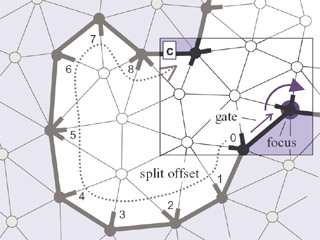
Although both schemes are guided by the same spiraling spanning tree, they process
triangles in a different order, making it difficult to understand their
similarities and to explain their varying compression success.
We describe a coding scheme that can operate like a label-based coder
similar to Edgebreaker or like a degree-based coder similar to the TG
coder. In either mode our coder processes vertices and triangles in the
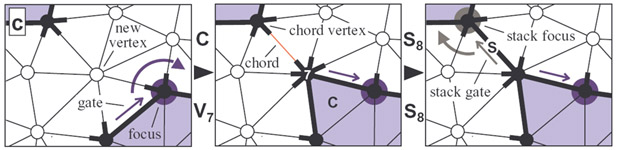
same order by performing the so-called ``split operations'' earlier than
previous schemes. The main
insights offered by this unified view are (a) that compression rates depend
mainly on the choice of decoding strategy and less on whether labels or
degrees are used and (b) how to do degree coding without storing ``split''
offsets. Furthermore we describe a new heuristic that allows
the TG coder's bit-rates to drop below the vertex degree entropy.
publication:
[is-esctmc-06.pdf slides] Martin Isenburg, Jack Snoeyink, Early-Split Coding for Triangle Mesh Connectivity, Proceedings of Graphics Interface 2006, pages 89-97, June 2006.
related publications:
[i-cpmcddp-02.pdf slides] Martin Isenburg, Compressing Polygon Mesh Connectivity with Degree Duality Prediction, Proceedings of Graphics Interface 2002, pages 161-170, May 2002.
[is-sr-00.pdf slides] Martin Isenburg, Jack Snoeyink, Spirale Reversi: Reverse decoding of the Edgebreaker encoding, Canadian Conference on Computational Geometry 2000, 247-256, August 2000.
---> appeared as a journal version in Computational Geometry, Volume 20, Issue 1-2, pages 39-52, October 2001.
downloads:
slides: esctmc.ppt


