Geometry Prediction for High Degree Polygons
Martin Isenburg Ioannis Ivrissimtzis Stefan Gumhold Hans-Peter Seidel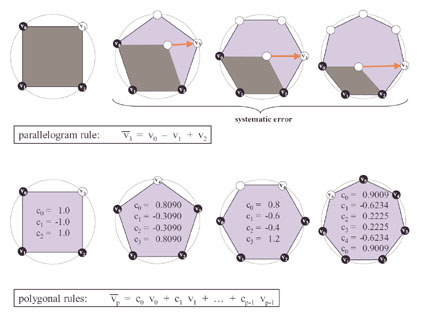

abstract:
The parallelogram rule is a simple, yet effective scheme to predict
the position of a vertex from a neighboring triangle. It was
introduced by Touma and Gotsman to compress
the vertex positions of triangular meshes. Later,
we showed that this rule
is especially efficient for quad-dominant polygon meshes when applied
within rather than across polygons. However, for hexagon-dominant
meshes the parallelogram rule systematically performs miss-predictions.
In this paper we present a generalization of the parallelogram
rule to higher degree polygons. We compute a Fourier decomposition
for polygons of different degrees and assume the highest frequencies
to be zero for predicting missing points around the polygon.
In retrospect, this theory also validates the parallelogram rule
for quadrilateral surface mesh elements, as well as the Lorenzo
predictor for hexahedral volume mesh elements.
main contributions:
publications:
related publications:
download:
funding: