Beacon Placement for Network Tomography
Research | Past Research Projects | Prototypes
Recent interest in using tomography for network monitoring has motivated the issue of whether it is possible to use only a small number of probing nodes (beacons) for monitoring all edges of a network in the presence of dynamic routing. Past work has shown that minimizing the number of beacons is NP- hard, and has provided approximate solutions that may be fairly suboptimal. In our work, we use a two-pronged approach to compute an efficient beacon set: (i) we formulate the need for, and design algorithms for, computing the set of edges that can be monitored by a beacon under all possible routing states; and (ii) we minimize the number of beacons used to monitor all network edges. We show that the latter problem is NP-complete and use various approximate placement algorithm that yields beacon sets of sizes within 1 + ln(|E|) of the optimal solution, where E is the set of edges to be monitored. Beacon set computations for several Rocketfuel ISP topologies indicate that our algorithms may reduce the number of beacons yielded by past solutions by more than 50% and are, in most cases, close to optimal.
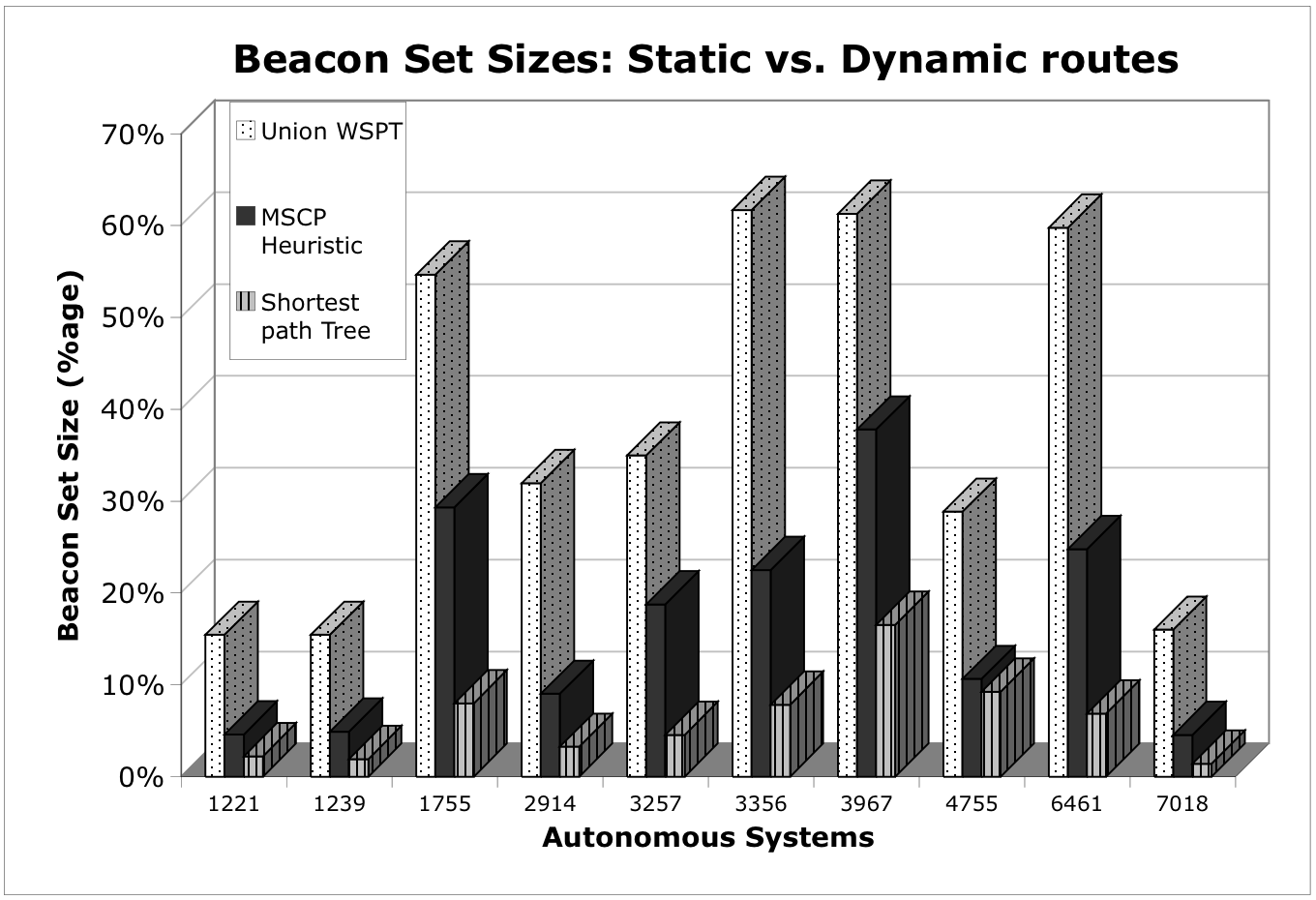
The following graph shows the results of our beacon set algorithms on 10 rocketfuel topologies. Note that our approach (the black and gray bars) yield much smaller beacon sets than previous approaches (the white bar).
The following graph shows the results of using a beacon placement algorithm for statically routed networks on 10 rocketfuel topologies. We observe that such an algorithm can perform very well (light gray bar with black vertical lines) on a statically routed network. However, for a fair comparison with our technique (which works on dynamically routed networks), we run the previous algorithm on 10 randomly generated routes (details in the paper) and take a union of all the resulting beacon sets for comparison. In dynamically routed networks, our technique (the dark gray bar) performs better than the union set computed (white bar with dots).