
This project is concerned with convex decompositions of polyhedra, particularly from the viewpoint of collision detection. So, what exactly is convex decomposition? Convex decomposition is the idea of "extracting" convexity from arbitrary polyhedra by splitting it up into convex pieces. This is an important problem because convex polyhedra are far easier to manipulate and deal with than nonconvex polyhedra. The complexity of applications such as collision detection increases drastically when given nonconvex polyhedra as input. There are several different ways to decompose polyhedra into convex pieces, and it is possible that certain decomposition algorithms yield better results than others for some applications.
How are convex decompositions computed? There are two broad categories of convex decomposition techniques:
Convex solid decomposition is known to have output of size O(n2) where n is the number of boundary elements of a polyhedron. This is impractical for real-time applications such as collision detection because of its quadratic complexity. Convex surface decomposition, on the other hand, is of complexity O(r) where r is the number of reflex (non-convex) edges in the surface. Decomposing polyhedra into the minimum number of convex pieces is known to be NP-complete, so heuristics are used to solve the problem.
There are several ways to perform convex surface decomposition. Some of these techniques are described in [1]:
Chazelle et al. divide flooding heuristics into two sub-groups: greedy flooding and controlled flooding. Greedy flooding heuristics collect faces until no adjacent face can be added without violating the convexity of the current patch being constructed. Controlled flooding heuristics have other stopping rules that can be other than simply convexity violation.
One of the decomposition algorithms (cresting BFS) used in SWIFT++ is a flooding algorithm with a seeding technique that prioritizes the nodes to start searching from in the dual graph. Once the nodes have been prioritized, convex patches are created by adding faces to the current convex patch until a convexity constraint is violated (the constraints are explained in more detail in [2]). The seeding technique involves choosing start faces that are distant from non-convex edges in the surface. This gives the patch more opportunity to grow. The idea is to try to minimize the number of patches by allowing them to grow as large as possible.
SWIFT++ uses a bounding volume hierarchy of convex hulls of convex pieces for proximity queries. It may be the case that using a different decomposition algorithm will provide performance benefits. One possible idea is to construct the hierarchy on convex pieces of relatively equal sizes (in terms of number of faces), or relatively equal surface areas.
To this end, one of the first ideas I thought of implementing was to allow pieces to grow until a certain threshold size had been reached, then cut them off and begin growing from another face. Another idea was to try to grow pieces in parallel. Before trying to implement either of these ideas, I tried some other things:
These are described in more detail in the next section.
These are the algorithms that I implemented:
Forward cresting
This algorithm is essentially the same as the cresting algorithm in SWIFT++, but with a slightly different distance calculation (SWIFT++'s calculation seemed to make some faces have slightly larger distances than they should have been).
Reverse cresting
This algorithm is as described in the previous section.
Face flooding (reverse and forward)
This algorithm uses potential piece sizes (number of faces) instead of distances from reflex edges. This data is calculated by flooding the mesh as follows:
In reverse face flooding, the faces in the pieces with smallest face count are given highest priority. This allows the smallest potential pieces to grow first, as in reverse cresting. Similarly, in forward face flooding, faces in pieces with higher face counts are given highest priority.
Area flooding (reverse and forward)
This algorithm is essentially the same as the face flooding algorithm, except instead of using the face count as the value for prioritization, each convex piece's surface area is used. Again, the reverse algorithm gives the smallest surface area the highest priority, and the forward algorithm gives the largest surface area the highest priority.
Face count and total area cutoff (sort of)
I attempted to implement the cutoff I described earlier in the Ideas section, but I ran into some issues so I was unable to obtain much useful data (described in next section).
I tested these algorithms on several models, but only had time to collect randomized test results on a relatively small model, as running many trials of decomposition algorithms on large models takes very long. The statistics that I was interested in were:
Below is a table of these statistics for 1000 randomized executions on a model of spoon. The spoon model has 336 triangles, 170 vertices, and 17 triangles with all 3 edges reflex.
| swift dfs | swift bfs | swift cresting | forward cresting | reverse cresting | forward face flood | reverse face flood | forward area flood | reverse area flood | |
| avg # of pcs | 80.602 | 78.991 | 77.834 | 78.352 | 78.131 | 86.004 | 81.232 | 84.405 | 84.454 |
| max # of pcs | 86 | 84 | 81 | 83 | 81 | 95 | 88 | 96 | 97 |
| min # of pcs | 76 | 76 | 76 | 76 | 75 | 81 | 79 | 76 | 77 |
| avg size of pcs | 4.1702 | 4.2548 | 4.3174 | 4.2895 | 4.3011 | 3.9088 | 4.1377 | 3.9874 | 3.9842 |
| std dev (pc size) | 5.9494 | 6.3408 | 6.2917 | 6.1725 | 5.9158 | 5.7004 | 5.3596 | 5.6359 | 5.6305 |
| avg # of size 1 pcs | 19.175 | 18.694 | 18.136 | 18.07 | 18.758 | 26.577 | 19.873 | 23.7 | 23.769 |
| avg # of size 2 pcs | 31.684 | 31.106 | 28.086 | 29.64 | 29.896 | 29.563 | 31.364 | 31.428 | 31.367 |
| avg surface area | 0.0084 | 0.0086 | 0.0087 | 0.0087 | 0.0087 | 0.0079 | 0.0084 | 0.0081 | 0.008 |
| std dev (surface area) | 0.0108 | 0.0112 | 0.011 | 0.0108 | 0.011 | 0.0102 | 0.0105 | 0.0105 | 0.0105 |
This data is not incredibly illuminating, as most of the results are relatively similar. However, the flooding algorithms in general produced a smaller standard deviation of piece sizes, but also a larger number of pieces overall. It is difficult to gauge the effectiveness of these algorithms without having tested them rigorously on multiple and varied models.
When I tried to implement the face count and area cutoff algorithms, I ran into problems of determining a threshold value. I originally intended to use a threshold based somewhat on the number of reflex edges present in the model. However, while an upper bound on the number of convex pieces needed relative to the number of reflex edges has been studied, a lower bound does not make as much sense. There are cases in which many faces (e.g. a triangle strip) are coplanar. If two of these triangle strips form a 'V' length-wise, then you only need to split them into two pieces, but the number of reflex edges will equal the number of edges adjacent to both triangle strips, which could be arbitrarily large depending on the number of triangles in each strip.
I later tried to implement the cutoff algorithms using the flooding technique. I used flooding to get an estimate of the average potential piece size, and intended to use this average piece size as the cutoff threshold. However, there does not seem to be a discernible direct relationship between the number of pieces required and the average piece size generated from flooding.
I did, however, test out the algorithm with a few other cutoff thresholds, but the thresholds were constant values and not based upon any algorithm. In general, lower cutoff thresholds led to smaller average piece sizes and smaller standard deviations, but a higher number of pieces. This makes sense, as each piece can no longer grow as much as it normally would have been able to.
There were also issues in trying to implement a parallel algorithm. The basic problem lies in determining how many (and which) pieces to grow from in parallel. Deciding on a number of pieces may cause you to end up with far more pieces than needed. Miguel Otaduy has a decomposition algorithm that is fairly good at dealing with these issues and also seems to generate relatively equal-sized pieces.
I also had some trouble with the flooding algorithms in general. The flooding algorithms tended to generate more pieces of size (face count) 1. This is visible in the following images. I think this can resolved with some further tweaking of the algorithms.
Cresting

Flooding
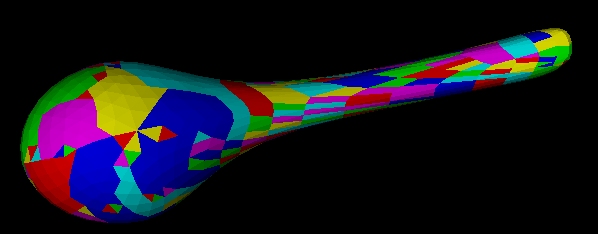
Originally, I had wanted to run timing tests in SWIFT++ similar to the ones in the EUROGRAPHICS 2001 paper [2] by replacing only the decomposition algorithms. This would give some indication of whether or not different decompositions make a difference. Unfortunately I lost some code last week that hadn't yet been backed up when I was working in Sitterson and the power went out, so I was not able to rigorously do such testing.
In the future, as mentioned, timing tests should definitely be done for various decomposition algorithms. It would be interesting to see if a combination of various techniques could be useful. It is also often the case that employing randomized algorithms can yield favorable results. It might be useful to test more randomized decomposition algorithms. For example, there is currently no randomization in the flooding phase of the flooding algorithms I implemented. The only randomization is introduced when the actual decomposition begins. Randomizing the flooding phase may produce better decompositions in the second phase. Clearly many tests also need to be done with a variety of different models.
Much thanks to Miguel Otaduy for his continual help with this project.
[1] Chazelle, B. et al. Strategies for polyhedral surface decomposition: An experimental study, Comp. Geom. Theory Appl., 7:327-342, 1997.
[2] Ehmann, Stephen A., Lin, Ming C. Accurate and Fast Proximity Queries Between Polyhedra Using Convex Surface Decomposition, EUROGRAPHICS 2001.
[3] Kim, Young J., Otaduy, Migual A., Lin, Ming C., Manocha, Dinesh. Fast Penetration Depth Computation for Physically-based Animation, ACM Symposium on Computer Animation, July 21-22, 2002.
[4] Lin, Ming C., Canny, John F. A Fast Algorithm for Incremental Distance Calculation, Proceedings of the 1991 IEEE International Conference on Robotics and Automation, April 1991.
[5] Chazelle, B. Convex Partitions of Polyhedra: A Lower Bound and Worst-Case Optimal Algorithm, SIAM J. Comp., Vol. 13, No. 3, August 1984.
[6] Bajaj, C. L., Dey, T. K., Convex Decomposition of Polyhedra and Robustness, SIAM J. Comp., Vol. 21, No. 2, April 1992.
[7] Kim, Young J., Lin, Ming C., Manocha, Dinesh. DEEP: Dual-space Expansion for Estimating Penetration Depth Between Convex Polytopes, Proc. IEEE International Conference on Robotics and Automation, May 11-15, 2002.