Final presentation slides - December 16, 2003
This project is an extension of the work done by Max Garber and Ming Lin in [1,2]. In those papers, they present a framework for motion planning of rigid and articulated bodies using a constrained dynamics [3] approach. It was my goal to extend this idea for use with multiple agents, particularly in conjunction with a higher-level behavioral model.
In [1,2], the motion of each rigid robot is influenced by virtual forces induced by geometric and other constraints. For articulated robots, joint connectivity and angle limits can be enforced by these constraints, and spatial relationships can be enforced between multiple robots. Constraints are divided into two major categories: hard constraints and soft constraints. Hard constraints must be satisfied at every time step in the simulation. Examples of hard constraints are non-penetration, articulated robot joint connectivity, and articulated robot joint angle limits. Soft constraints are used to encourage robots to behave in a certain way or proceed in certain directions. Examples of soft constraints are goal attraction, surface repulsion, and path following. The technique presented is used in dynamic environments with moving obstacles and is applicable to complex scenarios.
In addition to constraint-based motion planning, this project draws ideas from the behavioral modeling realm of research (e.g. Craig Reynolds' original flocking paper [4]). In particular, the generation of real-time dynamic autonomous agents is explored. There is much work that has been done in this area. As an example, Siome Goldenstein has presented a scalable methodology for agent modeling based on nonlinear dynamical systems and kinetic data structures [5,6]. In that paper, they used a three-layer approach: a local layer, a global environment layer, and a global planning layer. The local layer is responsible for modeling low-level behaviors using nonlinear dynamical systems theory. The global environment layer efficiently tracks each agent's immediate environment to provide nearby obstacle/agent information to help in behavioral decision-making. The global planning layer essentially implements target tracking and navigation through an environment while avoiding local minima.
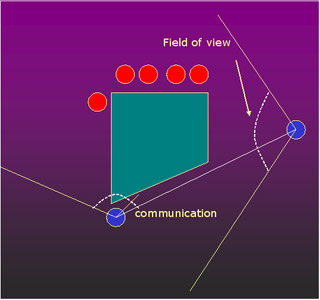
The purpose of this project is to extend the constraint-based motion planning system in [1,2] to allow for additional constraints that might be required in a multi-agent system, such as line-of-sight constraints. In addition, these multi-agent systems are controlled by a behavioral level that will incorporate ideas of information sharing between agents. One can imagine many situations in which multiple agents would have to interact with each other in order to accomplish a specified task. I am considering scenarios in which agent cooperation is not required but of great benefit to all agents, such as a military or capture-the-flag type situation. There are cases in which information shared between multiple agents can be very beneficial. As a simple example, the figure below shows two opposing teams.

The left blue agent, when peeking around the corner, can see one red agent, but knows nothing about the other four red agents waiting around the other side of the central barrier. The right blue agent, on the other hand, knows that there are four more red agents there. If the two blue agents have line of sight and can communicate (assuming a simple case where other types of communication are not possible), then this information can be combined to give both agents an effectively larger view of the environment.
In an ideal situation, a team would like to know as much about its environment as possible in order to generate a viable plan of action. This implies that the agents should spread out across the environment such that their combined view will cover as much of the environment as possible. However, there are also situations in which the agents may need to hide due to immediate danger, such as entering the line of sight of an enemy.
My goals were to take these high-level behaviors and map them into constraints in a situation in which motion planning must be driven by more than just reaching an end goal. I also wanted to look at what can be done in the case of having incomplete information about where the obstacles (enemies) are, or information that becomes invalid over time (e.g. if an agent looks at one area and sees an enemy and then turns away, the potential location of the enemy over time becomes less and less certain).
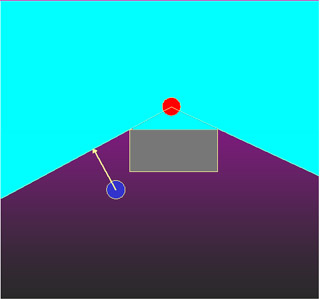
The primary mechanism I attempted to implement was the line-of-sight (LOS) constraint. The basic LOS problem I wanted to solve is characterized as follows:
For this problem, I initially assumed that the agents have full knowledge of the static environment, but do not know about dynamic parts of the environment (such as enemies or moving obstacles) until they have been seen.
In order to bring an enemy back into view, I try to have agents move to the closest point where the enemy will be visible again. Again, the agent is the blue circle and the enemy is the red circle. The cyan region shows the set of points that are visible (omnidirectionally) from the enemy's position. The agent will try to move to the closest point in this visibility region. Since agents know the static environment, they essentially know from where points in the environment can be seen (i.e., they have a global roadmap of sorts, but no roadmap is explicitly computed).
The basic algorithm that I use is given in the following pseudocode:
if agent does not see enemy and does not know enemy location {
patrol area until enemy seen;
}
else {
determine enemy's visibility volume based on predicted position and velocity;
move agent towards closest point in volume;
}
In general, when an agent has any information about an enemy's whereabouts, it can use the enemy's last known position and velocity to predict enemy movement and determine the enemy's visibility region. If one agent does not know the enemy's location but another agent does, then these agents share this information. Agents can also have a hard constraint of line of sight between them. This constraint means that they cannot move such that they are out of line of sight. This is essentially equivalent to having a rigid bar (of varying length) connecting the two agents such that the bar can never intersect any obstacles in the environment.
Using the knowledge paradigm, this technique can also be used to allow for moving obstacles in the environment as well as moving agents/enemies. Agents can use the last known state of obstacles in the environment to predict their next state and compute visibility using that information.
I implemented these ideas by extending Max Garber's CPLAN system. I use NV_OCCLUSION_QUERY in order to determine if an enemy is currently visible from the agent's position. If the occlusion query returns that no fragments of the enemy are visible from the agent's position, then the enemy is not in the agent's line of sight.
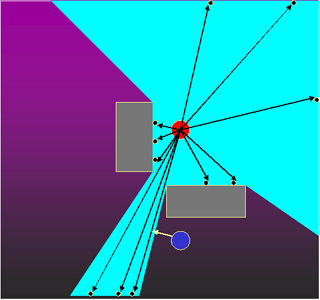
If the agent has some knowledge of where the enemy is (either from a previous sighting or from a friendly agent who has recently seen the enemy), then it predicts the enemy's next position, and determines what set of points in the environment are able to see the predicted position without occlusion. This visibility region is computed by rendering the environment from the enemy's point of view in all directions using 90-degree view frusta: left, down, right, up, above, and below (currently above and below are not being done, but the other 4 views include some information about points above and below the enemy).
Once these different views are rendered, I read back the depth buffer from each view. Given the depth buffer from each view, I then sample points uniformly in each buffer, and determine the world-space ray that each sampled point corresponds to (see the figure below). The sampling attempts to capture the extent of the visibility volume. The agent determines which world-space ray it is closest to, and sets a soft constraint attractive goal to move towards the closest point on that ray.
Since I am reading back the depth buffer, these operations are costly. Instead of doing this computation in every time step, I do it once every N time steps, where N is a parameter to the simulation. The agent moves towards the last computed closest point until N time steps have passed, and then if the enemy is still not in view, the enemy's visibility region is recomputed and a new closest point is determined. Note that if N is too high, then the visibility region will often be "stale", and if N is too low, then the agent will be prone to moving more randomly since ray samples may vary widely with each computation.
Below are several videos showing the results of using this technique. In each of these videos (except for newscene2.avi) the agent(s) are red and the enemy is a bluish color. In newscene2.avi, the agent is blue and the enemy is red. The cyan line shown connects an agent with the enemy it is trying to keep in its line of sight. When you see many yellow lines appear, the enemy has gone out of sight and the visibility region is being sampled. The yellow lines represent the world-space rays resulting from the sampling. (Note that due to a rendering bug, the world-space rays follow the enemy in the scene, even though they are supposed to remain stationary in the environment for N time steps.) In each case, 512 ray samples were taken per depth buffer. Each image was rendered at a resolution of 512x512.
|
|
newscene1.avi (8187904 bytes)
This scene shows an enemy moving past a single corner to get away from the agent. N was set to 50. |
|
|
newscene2.avi (6926336 bytes)
This scene shows an enemy (bluish) moving past a single corner to get away from the agent (red). N was set to 50. |
|
|
newscene3.avi (11674624 bytes)
This scene is slightly more complex, because the enemy (bluish) goes through a narrower passage between obstacles, and the agent (red) must keep line of sight through this more restricted region of the environment. N was set to 250. |
|
|
newscene4.avi (7204864 bytes)
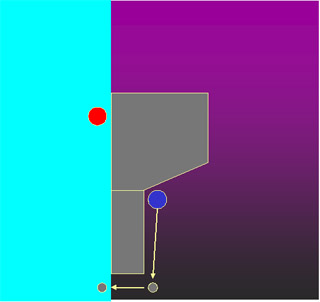
This scene shows several agents (red) cooperating. Initially only one agent can see the enemy (bluish). The agent on that initially sees the enemy communicates its information to the other agents, and the last agent attempts to go around the obstacle to reach the enemy. At the same time, all the agents try to stay within the line of sight of each other. N was set to 50. |
Numerical (im)precision is always a problem, and this case is no different. The imprecision of the depth buffer leads to many rays that are not properly represented (e.g. rays that appear to go through obstacles). Also, as with any dynamic simulation, there are often many parameters that need to be tweaked in order to get reasonable results. For example, care must be taken to set the repulsive forces of obstacles properly such that they do not prevent the line-of-sight goal constraints from being satisfied. Additionally, the sampling technique is not an exact solution, and as such does not find the actual closest point to the visibility region.
Overall, this technique seems to give reasonable results. However, there are several things that can be changed:
[1] Garber, M. and Lin, M. Constraint-Based Motion Planning using Voronoi Diagrams. Proc. Fifth International Workshop on Algorithmic Foundations of Robotics (WAFR), 2002.
[2] Garber, M. and Lin, M. Constraint-Based Motion Planning for Virtual Prototyping. Proc. ACM Symposium on Solid Modeling and Applications, 2002.
[3] Witkin, A. and Baraff, D. Physically Based Modeling: Principles and Practice. ACM Press, 1997. Course Notes of ACM SIGGRAPH.
[4] Reynolds, C. W.. Flocks, Herds, and Schools: A Distributed Behavioral Model. Computer Graphics, 21(4): 25-34, 1987.
[5] Goldenstein, S., Large, E., and Metaxas, D. Dynamic Autonomous Agents: Game Applications. Computer Animation, 1998.
[6] Goldenstein, S., Karavelas, M., Metaxas, D., Guibas, L., Aaron, E., and Goswami, A. Scalable nonlinear dynamical systems for agent steering and crowd simulation. Computer and Graphics, 25(6): 983-998, 2001.
[7] Stout, B. Smart move: Path-finding. Game Developer, Oct. 1996.
[8] Vinckle, S. Real-time pathfinding for multiple objects. Game Developer, June 1997.
[9] Pottinger, D. Coordinated unit movement. Game Developer, Jan. 1999.
[10] Gonzales-Banos, H.H., Lee, C.Y., and Latombe, J.C. Real-Time Combinatorial Tracking of a Target Moving Unpredictably Among Obstacles. Proc. IEEE Int. Conf. on Robotics and Automation, Washington DC, May 2002.