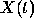 and
and 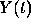 .
.



Let us suppose that a child is walking on the plane. His orbit is
given by the two functions of time 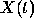 and
and 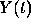 .
.
Suppose now that the child is pulling some toy, to which he is connected
by a rigid bar of length a. We are interested in computing the orbit of
the toy when the child is walking around. Let 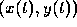 be the
position of the toy. Based on these relationships we can formulate the
following equations:
be the
position of the toy. Based on these relationships we can formulate the
following equations:
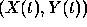 and
and 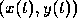 is
always the length of the bar. Therefore
is
always the length of the bar. Therefore
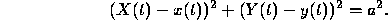
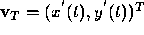 :
:
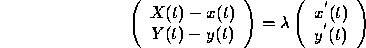
with 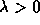 .
.
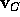 . Assume e.g.
that the child is walking on a circle of radius a (length of the bar).
In this special case the toy will stay in the center of the circle and not
move at all.
. Assume e.g.
that the child is walking on a circle of radius a (length of the bar).
In this special case the toy will stay in the center of the circle and not
move at all.
In general, the absolute value of the velocity of the toy is given by the absolute value of the projection of the velocity of the child onto the bar.