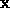 .
.
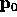 and
and 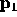 have to be extremas (points). For example, if
have to be extremas (points). For example, if 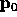 is not an extremal point, the algorithm may not terminate.
Similarly if
is not an extremal point, the algorithm may not terminate.
Similarly if 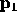 is not an extremal point, it will be popped out of the
stack.
is not an extremal point, it will be popped out of the
stack.



The algorithm presented assumes two things:
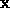 .
.
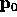 and
and 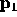 have to be extremas (points). For example, if
have to be extremas (points). For example, if 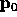 is not an extremal point, the algorithm may not terminate.
Similarly if
is not an extremal point, the algorithm may not terminate.
Similarly if 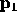 is not an extremal point, it will be popped out of the
stack.
is not an extremal point, it will be popped out of the
stack.
To get around the second problem, we modify the algorithm somewhat. The main idea is to compute a point on the hull (say the one with minimal y coordinate). All the points are sorted with respect to this point on the hull. We label the points based on this sorting and use it to initialize two points on the stack.
The modified version of Graham's algorithm is:
Algorithm
Find rightmost lowest point; label it 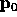 .
.
Sort all other points angularly about 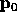 ,
,
 break ties in favor of closeness to
break ties in favor of closeness to 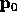 ;
;
 label
label 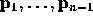 .
.
Stack 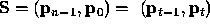 ; t indexes top
; t indexes top
i = 1
while  do
do
 if
if 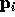 is left of
is left of 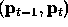
 then Push(
then Push(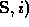 and
increment i.
and
increment i.
 else Pop(
else Pop(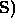 .
.
Its complexity is 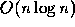 .
.