


Next: Incremental Algorithm
Up: Graham's Algorithm
Previous: Degeneracies
In terms of implementation, we address two main issues:
- Implementation using floating point arithmetic? What are likely sources
of error or inconsistent arithmetic?
- Implementation using integer point aritmetic? Suppose the input is
given as integer coordinates, we would like to avoid any floating point
arithmetic. In particular, the computation of angles (for sorting) involves
computing the
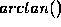 or
or 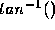 function. Its input is a double
precision number, so it involves converting from int to double. This
could be inaccurate if the machine allocates more bits to the int type
than it does to the mantissa of the double type. Furthermore, the
function. Its input is a double
precision number, so it involves converting from int to double. This
could be inaccurate if the machine allocates more bits to the int type
than it does to the mantissa of the double type. Furthermore, the
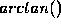 function only computes an approximation to the irrational number.
Instead of using
function only computes an approximation to the irrational number.
Instead of using 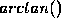 , we can use the slopes. For that we need to make
sure, that the lines are in appropriate quadrants. More details are given
in Section 1.5.2 of O'Rourke's book.
, we can use the slopes. For that we need to make
sure, that the lines are in appropriate quadrants. More details are given
in Section 1.5.2 of O'Rourke's book.
Implementation of Left: Given 3 points,
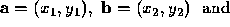
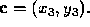 The point
The point  is left of
is left of
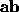 , if
, if
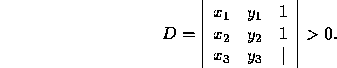
 is collinear with
is collinear with 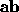 , if D = 0.
, if D = 0.
Optimal Convex Hull Algorithm:
The most optimal algorithm for convex hulls is due to
Seidel & Kirkpatrick (1981). Its complexity is 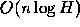 , where H
is the number of extreme points in the input. It is output sensitive.
, where H
is the number of extreme points in the input. It is output sensitive.
Dinesh Manocha
Tue Feb 17 23:44:05 EST 1998
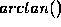 or
or 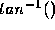 function. Its input is a double
precision number, so it involves converting from int to double. This
could be inaccurate if the machine allocates more bits to the int type
than it does to the mantissa of the double type. Furthermore, the
function. Its input is a double
precision number, so it involves converting from int to double. This
could be inaccurate if the machine allocates more bits to the int type
than it does to the mantissa of the double type. Furthermore, the
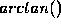 function only computes an approximation to the irrational number.
Instead of using
function only computes an approximation to the irrational number.
Instead of using 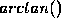 , we can use the slopes. For that we need to make
sure, that the lines are in appropriate quadrants. More details are given
in Section 1.5.2 of O'Rourke's book.
, we can use the slopes. For that we need to make
sure, that the lines are in appropriate quadrants. More details are given
in Section 1.5.2 of O'Rourke's book.



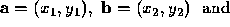
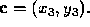 The point
The point  is left of
is left of
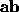 , if
, if
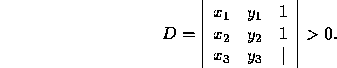
 is collinear with
is collinear with 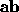 , if D = 0.
, if D = 0.
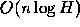 , where H
is the number of extreme points in the input. It is output sensitive.
, where H
is the number of extreme points in the input. It is output sensitive.