


Next: Vector and Matrix
Up: No Title
Previous: No Title
Linear algebra is perhaps the most important tool in scientific computing.
We will start with a quick review of linear algebra. Notation:
- Upper case bold-face like
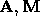 are used to represent matrices.
are used to represent matrices.
- Lower case bold-face like
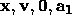 are used to represent vectors.
are used to represent vectors.
- Scalars are represented using standard fonts (like
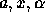 ).
).
-
 is used to represent identity matrix.
is used to represent identity matrix.
-
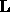 is used to represent a lower triangular matrix.
is used to represent a lower triangular matrix.
-
 is used to represent an upper triangular matrix.
is used to represent an upper triangular matrix.
-
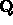 is used to represent an orthogonal real matrix.
is used to represent an orthogonal real matrix.
-
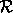 represents the set of real numbers.
represents the set of real numbers.
Given an 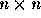 real matrix,
real matrix, 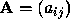 , we denote its inverse by
, we denote its inverse by 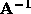 and the determinant by
and the determinant by 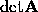 . If the determinant is non-zero,
the matrix is non-singular. For a given non-singular matrix, the
following results are equivalent:
. If the determinant is non-zero,
the matrix is non-singular. For a given non-singular matrix, the
following results are equivalent:
- A is non-singular.
-
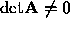 .
.
- The linear system
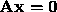 has the only solution
has the only solution
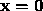 .
.
- For any vector b, the linear system
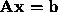 has a
unique solution.
has a
unique solution.
- The columns (rows) of
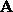 are linearly independent; that is, if
are linearly independent; that is, if
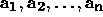 are the columns of
are the columns of 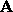 and
and
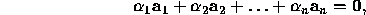
then all the scalars 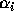 are necessarily zero.
are necessarily zero.
-
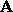 has rank n, where the rank of a matrix is the number of
linearly independent rows or columns.
has rank n, where the rank of a matrix is the number of
linearly independent rows or columns.
The transpose of  is
is 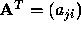 . A matrix
. A matrix
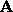 is symmetric if
is symmetric if 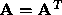 . Furthermore, if for
all vectors
. Furthermore, if for
all vectors 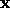 ,
, 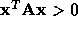 ,
, 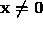 ,
then
,
then 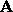 is positive definite.
is positive definite.
A submatrix of 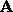 is obtained by deleting rows and columns of
is obtained by deleting rows and columns of
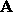 . A principal submatrix results from deleting corresponding
rows and columns. A leading principal submatrix of size k is obtained
by deleting rows and columns
. A principal submatrix results from deleting corresponding
rows and columns. A leading principal submatrix of size k is obtained
by deleting rows and columns  .
.
Eigenvalues and Eigenvectors: The eigenvalues and eigenvectors of
a matrix are the solutions to the following matrix equation:

where 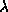 is the eigenvalue and
is the eigenvalue and 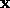 is the eigenvector. The
eigenvalues are the roots of the polynomial equation:
is the eigenvector. The
eigenvalues are the roots of the polynomial equation:

This is the characteristic equation of 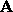 and is a polynomial
of degree n in
and is a polynomial
of degree n in 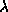 . As a result,
. As a result, 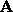 has precisely n
eigenvalues. Notice that the problem of computing the eigenvalues is
well-conditioned for most cases and stable algorithms are known for it.
On the other hand the problem of finding roots can be ill-conditioned.
The stable algorithms for eigenvalue computation DO NOT reduce the problem
to finding roots of its characteristic polynomial.
has precisely n
eigenvalues. Notice that the problem of computing the eigenvalues is
well-conditioned for most cases and stable algorithms are known for it.
On the other hand the problem of finding roots can be ill-conditioned.
The stable algorithms for eigenvalue computation DO NOT reduce the problem
to finding roots of its characteristic polynomial.



Next: Vector and Matrix
Up: No Title
Previous: No Title
Dinesh Manocha
Mon Jan 27 13:16:15 EST 1997
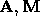 are used to represent matrices.
are used to represent matrices.
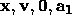 are used to represent vectors.
are used to represent vectors.
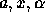 ).
).
 is used to represent identity matrix.
is used to represent identity matrix.
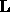 is used to represent a lower triangular matrix.
is used to represent a lower triangular matrix.
 is used to represent an upper triangular matrix.
is used to represent an upper triangular matrix.
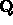 is used to represent an orthogonal real matrix.
is used to represent an orthogonal real matrix.
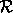 represents the set of real numbers.
represents the set of real numbers.
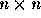 real matrix,
real matrix, 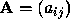 , we denote its inverse by
, we denote its inverse by 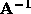 and the determinant by
and the determinant by 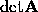 . If the determinant is non-zero,
the matrix is non-singular. For a given non-singular matrix, the
following results are equivalent:
. If the determinant is non-zero,
the matrix is non-singular. For a given non-singular matrix, the
following results are equivalent:
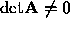 .
.
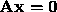 has the only solution
has the only solution
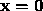 .
.
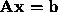 has a
unique solution.
has a
unique solution.
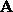 are linearly independent; that is, if
are linearly independent; that is, if
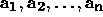 are the columns of
are the columns of 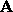 and
and
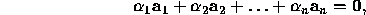
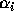 are necessarily zero.
are necessarily zero.
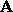 has rank n, where the rank of a matrix is the number of
linearly independent rows or columns.
has rank n, where the rank of a matrix is the number of
linearly independent rows or columns.
 is
is 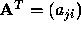 . A matrix
. A matrix
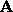 is symmetric if
is symmetric if 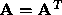 . Furthermore, if for
all vectors
. Furthermore, if for
all vectors 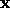 ,
, 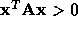 ,
, 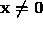 ,
then
,
then 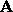 is positive definite.
is positive definite.
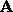 is obtained by deleting rows and columns of
is obtained by deleting rows and columns of
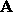 . A principal submatrix results from deleting corresponding
rows and columns. A leading principal submatrix of size k is obtained
by deleting rows and columns
. A principal submatrix results from deleting corresponding
rows and columns. A leading principal submatrix of size k is obtained
by deleting rows and columns  .
.

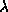 is the eigenvalue and
is the eigenvalue and 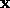 is the eigenvector. The
eigenvalues are the roots of the polynomial equation:
is the eigenvector. The
eigenvalues are the roots of the polynomial equation:

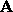 and is a polynomial
of degree n in
and is a polynomial
of degree n in 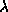 . As a result,
. As a result, 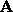 has precisely n
eigenvalues. Notice that the problem of computing the eigenvalues is
well-conditioned for most cases and stable algorithms are known for it.
On the other hand the problem of finding roots can be ill-conditioned.
The stable algorithms for eigenvalue computation DO NOT reduce the problem
to finding roots of its characteristic polynomial.
has precisely n
eigenvalues. Notice that the problem of computing the eigenvalues is
well-conditioned for most cases and stable algorithms are known for it.
On the other hand the problem of finding roots can be ill-conditioned.
The stable algorithms for eigenvalue computation DO NOT reduce the problem
to finding roots of its characteristic polynomial.