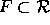Floating Point Number System

A floating point number system 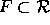is a subset of the real numbers whose elements have the form

The system F is characterized by four integer parameters:

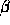• the base (sometimes called the radix),
• the precision t, and
• the exponent range .

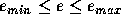The mantissa m is an integer satisfying 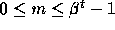. To ensure a unique representation for each 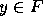, it is assumed that 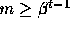if 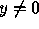, so that the system is normalized. In other words the first digit of the mantissa is non-zero. The range of the non-zero floating point numbers in F is given by

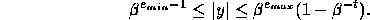
It follows that every real number x lying in the range of F can be approximated by an element of F with a relative error no larger than 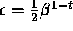. The quantity is called the machine epsilon or unit roundoff. It is the most useful quantity associated with F and is ubiquitous in the world of rounding error analysis.

We are mainly interested in IEEE floating point number system. Over the last few years it has become a standard.

IEEE Single Precision Arithmetic

  
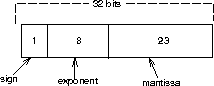
Figure 1: IEEE Single Precision Arithmetic

Based on these values the various parameters are:

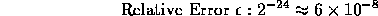
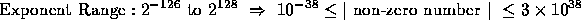
IEEE Double Precision Arithmetic

  
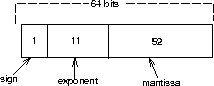
Figure 2: IEEE Double Precision Arithmetic

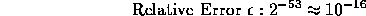
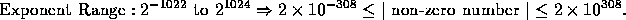
Roundoff error results since the true value of 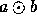, where 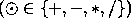can't be represented exactly and needs to be rounded off. If we roundoff as accurate as possible, and the floating point result is within the exponent range than

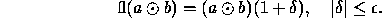
We say that fl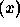 overflows if 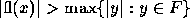and underflows if 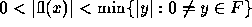. To see the impact of rounding and truncation, lets consider the following C program.

#include <stdio.h>
#include <math.h>

main()
{

    float f;
    double d,p;
    int i;

    i = 32768 * 32768 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1;
    f = (float) i;
    d = (double) i;

    p = fabs(f - i)/i;


    printf("%d  %4.16f %4.16lf %4.16f \n",i,f,d,p);

}