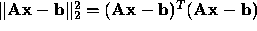 and look for
and look for  where the gradient of the function vanishes.
Let
where the gradient of the function vanishes.
Let  be
the set of vectors in the local neighbourhood of
be
the set of vectors in the local neighbourhood of  . For a minima,
we want
. For a minima,
we want



Consider
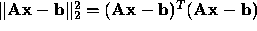 and look for
and look for  where the gradient of the function vanishes.
Let
where the gradient of the function vanishes.
Let  be
the set of vectors in the local neighbourhood of
be
the set of vectors in the local neighbourhood of  . For a minima,
we want
. For a minima,
we want
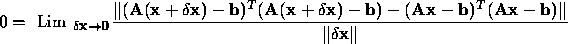
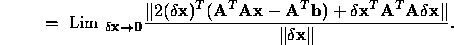
The second term in the above formula converges to zero (as shown below):
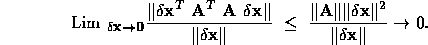
Therefore, the gradient is zero at the solution of:

or

The above system of n linear equations in n unknowns are
known as the normal equations. The matrix 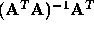 is also known as the pseudo-inverse of
is also known as the pseudo-inverse of 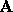 . The minimum
of the least square system corresponds to
. The minimum
of the least square system corresponds to
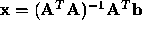 .
.
NOTE: 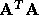 is s.p.d.
is s.p.d.  we can use Cholesky
decomposition (
we can use Cholesky
decomposition (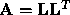 ). The overall cost would
be
). The overall cost would
be 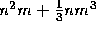
Why is 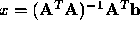 the minimum ?
the minimum ?
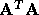 is positive definite ( a
necessary condition for the minima).
is positive definite ( a
necessary condition for the minima).
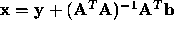 =
=
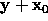 . After we substitute this solution in the
original set of linear equations and simplify, we obtain:
. After we substitute this solution in the
original set of linear equations and simplify, we obtain:
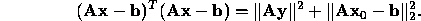
So clearly 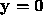 obtains a minima.
obtains a minima.