


Next: Linear Algebra Libraries
Up: Linear Least Square
Previous: QR Decomposition
The algorithms based on normal equations and QR decomposition only work
for fully-ranked input matrices (i.e. rank(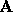 ) = n). If
) = n). If
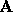 is rank-deficient, that there are infinite number of solutions to
the least squares problems and we can use algorithms based on SVD's. In
particular, if
is rank-deficient, that there are infinite number of solutions to
the least squares problems and we can use algorithms based on SVD's. In
particular, if 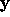 is a least square minimizer to the input system,
than
is a least square minimizer to the input system,
than 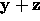 is also a minimizer, where
is also a minimizer, where  belongs to
the kernel of
belongs to
the kernel of 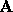 .
.
Given the SVD: 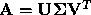 , the minimal
solution corresponds to:
, the minimal
solution corresponds to:

In practice, computation of SVD can take about 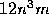 operations.
operations.
Dinesh Manocha
Tue Feb 3 23:49:47 EST 1998
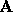 ) = n). If
) = n). If
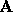 is rank-deficient, that there are infinite number of solutions to
the least squares problems and we can use algorithms based on SVD's. In
particular, if
is rank-deficient, that there are infinite number of solutions to
the least squares problems and we can use algorithms based on SVD's. In
particular, if 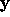 is a least square minimizer to the input system,
than
is a least square minimizer to the input system,
than 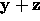 is also a minimizer, where
is also a minimizer, where  belongs to
the kernel of
belongs to
the kernel of 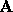 .
.



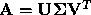 , the minimal
solution corresponds to:
, the minimal
solution corresponds to:

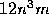 operations.
operations.