Visibility polygon

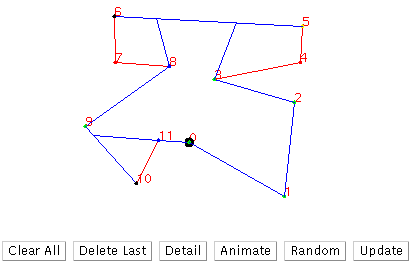
Enter vertices of a SIMPLE polygon in counter-clockwise (CCW) order. After clicking Update, the visibility polygon of vertex 0 is shown in blue.

I made some modifications to the linear time algorithm of ElGindy and Avis, "A linear algorithm for computing the visibility polygon from a point", J. Algorithms 2, 1981, p. 186--197. I use only one stack instead of three, store only original vertices to maintain tight control of numerical complexity, handle degenerate inputs, and correctly handle spirals of more than 360 degrees. These may be similar to Joe's corrections to Lee's algorithm (B. Joe and R. B. Simpson, "Correction to {Lee}'s visibility polygon algorithm", BIT, 27, 1987, p. 458--473.), but I don't have access to BIT at the moment to check.

To emphasize that the data structure uses only original polygon vertices (for numerical robustness), the display may look non-simple. To interpret the output at right, the circled p0 is the orgin, green (0,1,2,3,9) and blue (8,11) vertices are visible endpoints of visible edges, with blue indicating that the previous edge is not visible. Yellow (5) and black (6,10) are invisible endpoints of visible edges.

Known bugs: The polygon is not checked for simplicity or orientation, so entering a non-simple, or CW oriented polygon will cause strange results and error messages on the Java console. (I think I catch all possible infinite loops.)

• Detail toggles the vertex numbers and some of the edge weights.
• Animate toggles the behavior of Update: Either the visibility polygon for vertex 0 is computed, or visibility polygons for each vertex are computed and displayed for two seconds.
• Update is the button you push when the input is ready
• Clear All and Delete Last give minimalist editing.

Code by Jack Snoeyink, University of British Columbia. Back to Jack's Computational Geometry Demo page.