Physically-Based Modeling, Simulation and Animation
Assignment 1: ODE’s & Particle Dynamics

Zhen Wei

September 19, 2016

PIC

PIC

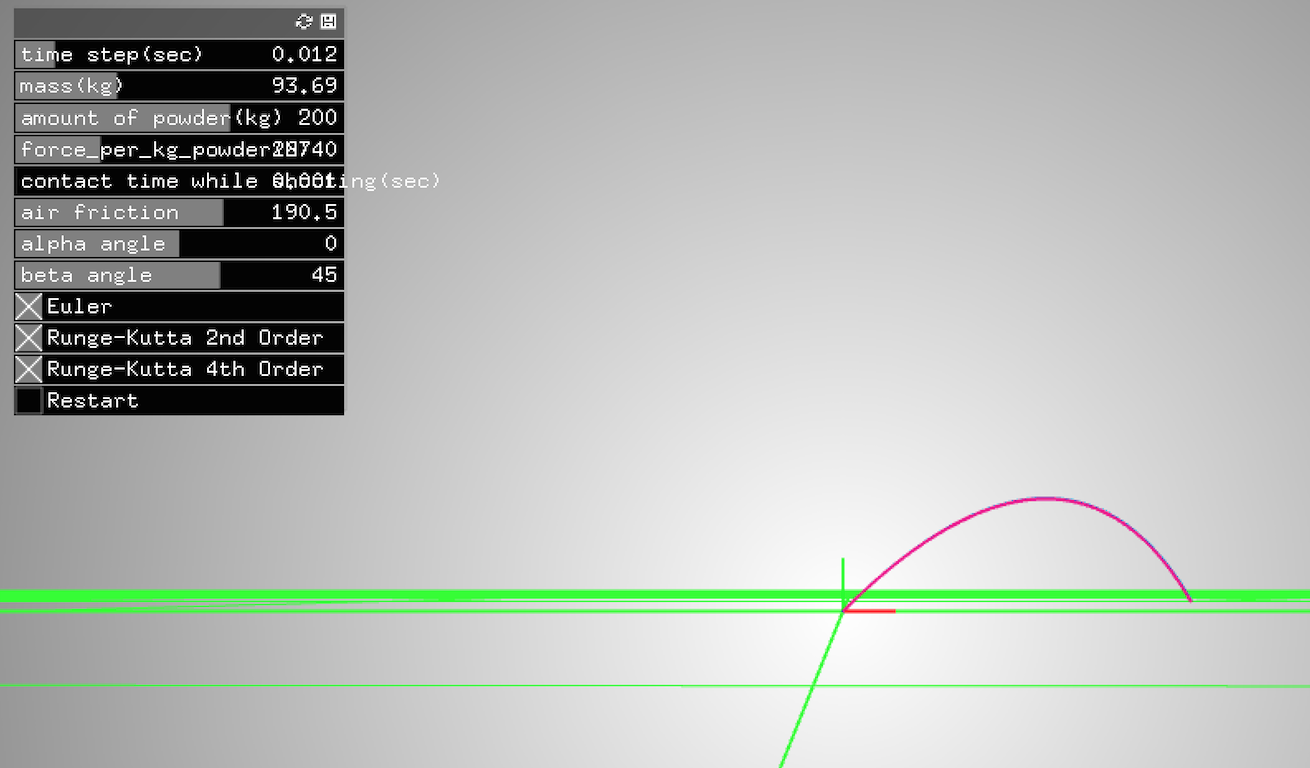
Problem A: Ballistic Motion Given a location of a gun at (0,0,0), write an 3D artillery simulator that can take in the mass of the projectile, amount of powder, the azimuth and elevation of the gun barrel. Use the amount of powder and the mass of the projectile to determine the muzzle velocity. Account for gravity and air friction. Assume that one kilogram of powder produces 10,000 newtons of force. Assume instantaneous acceleration as a result of the powder going off. Air friction coefficient is constant. Set it to be 50 kg/s initially. The gun and target are both on the X-Z plane.

Analysis: For analysis part, without loss of generality, we consider the condition without air friction for simplicity. The accumulate distances errors at time 10 sec and computation time for 500 * Δt are shown as follows, which are generated by Euler, 2nd Order Runge-Kutta, 4th Order Runge-Kutta Method in different time steps.

Table 1: Error Analysis: at time 10.0 sec, air_friction = 0, mass = 2kg, amount of powder = 200kg, force_per_kg_powder=1000N, contact_time_while_shooting= 0.001 sec, alpha angle = 0∘, beta angle = 45∘

Distance Error Euler RK2 RK4
Δt = 0.001 0.025925 0.023148 0.023117
Δt = 0.01 0.491989 0.001846 0.001846
Δt = 0.1 4.899979 0.000031 0.000031

Table 2: Computation Time Analysis: the time consumed after computing 500 * Δt, air_friction = 0, mass = 2kg, amount of powder = 200kg, force_per_kg_powder=1000N, contact_time_while_shooting= 0.001 sec, alpha angle = 0∘, beta angle = 45∘

Computation Time(μs) Euler RK2 RK4
Δt = 0.001 81 190 532
Δt = 0.01 89 211 565
Δt = 0.1 67 157 444

Problem B: Spring-Mass Simulator A spring hands vertically in its equilibrium or resting position. Given a user-defined mass m attached to the spring with the spring constant k, not stretched at first. Simulate the motion of the spring and mass under the effects of spring and gravitational forces. Assume the mass is 5 kg and k = 15kg∕s2. Then, set the mass to be 10 kg and k = 20kg∕s2.

Analysis: Without loss of generality, we consider the condition without damping for simplicity. The accumulate distances errors at time 10 sec and computation time for 500 * Δt are shown as follows, which are generated by Euler, 2nd Order Runge-Kutta, 4th Order Runge-Kutta Method in different time steps.

Table 3: Error Analysis: at time 10.0 sec, mass = 5kg, hook_k = 15kg∕s2.

Distance Error Euler RK2 RK4
Δt = 0.001 0.001997 0.000023 0.000000
Δt = 0.01 0.015499 0.002834 0.000002
Δt = 0.01 1.970125 0.283945 0.000417

Table 4: Computation Time Analysis: the time consumed after computing 500 * Δt, mass = 5kg, hook_k = 15kg∕s2.

Computation Time(μs) Euler RK2 RK4
Δt = 0.001 54 135 428
Δt = 0.01 56 139 400
Δt = 0.1 64 128 402

Summary: Euler Method is much more efficient, but also generate much more errors and is more unstable than the other ones. 4th-Order Runge-Kutta Method is more accurate than 2nd-Order one(Mid Point), while need more computation time than 2nd-Order(Mid Point).