Write a classical ray tracer like the one from Turner Whitted's 1980 paper. (assignment)
I extended my simple raytracer from COMP 236. I integrated the model parser provided in class and modiefied my previous illumination model. I also refactored a lot of the code in view of the later extensions I will implement for the next assignments.
In "An Improved Illumination Model for Shaded Display", Whitted presents a new illumination model in which the instensity at apoint is computed as follows:
![]()
where:
- Ia is the ambient light of the object
- kd is the diffuse reflection constant
- nls is the number of lights in the scene
- N is the normal at the point of intersection
- Lj is the normalized vector in the direction
of the light j in the scene
- ks is the specular reflection constant
- R is the intensity of light being reflected from other objects in the
scene to this point (reflection)
- kt is a light transmission constant
- T is the intensity of light being transmitted through the intersected
object (refraction).
For this assignment, I use a slightly modified model. The specular term is computed differently:
![]()
where:
- Rj is the normalized vector to light source
j reflected about the normal
- V is the normalized vector towards the source of the incoming ray
- ns is the power of the specular highlights
The R and T terms are computed by recursively shooting a "reflected"
and a "refracted" ray at each point. The following figures (taken
form Paul Rademacher's "Ray
Tracing: Graphics for the Masses") illustrate the principle:
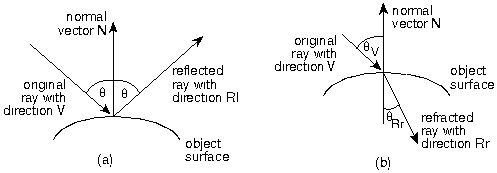
For each point I compute: a reflected ray (a) and a refracted ray (b).
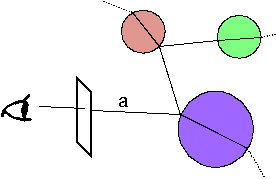
The result is a "ray tree", implemented with recursive calls.
For this assignment I used point light sources. Normally, if a light source is not "seen" from a point, the point does not receive light from that source. This results in hard shadows, which is reasonable only if objects are not transparent. The problem is that a reflected ray from a point has a very small probability of hitting a point light, and most of the time it just returns the background color. To make the images look more realistic, I applied a "trick" that is not justified mathematically, but produces better-looking results. If a ray from a point to a light source intersects a transparent object, I still compute the contribution of that light (even if the point is in the light's "shadow"), but I multiply it with the transparency coefficient of the intersected object.
Below are some screenshots produced by my program and an animation generated as a succession of images:
|
A screenshot the first model. |
|
A screenshot of the second model, with hard shadows. |
|
A screenshot of the second model, with "pseudo-soft" shadows. |
|
An animation of the camera moving around the first model. |