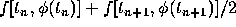 . This is equivalent to
approximating the area under the curve between
. This is equivalent to
approximating the area under the curve between 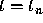 and
and 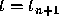 by the area of the shaded trapezoid. Further, we replace
by the area of the shaded trapezoid. Further, we replace 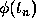 and
and
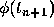 by their respective approximate values
by their respective approximate values 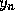 and
and 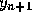 in this way we obtain from Eq. (11)
in this way we obtain from Eq. (11)



A better approximation method can be obtained if the integrand in
Eq. (11)
is approximated more accurately. One way to do this is to replace the
integrand by the average of its values at the two endpoints, namely,
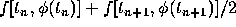 . This is equivalent to
approximating the area under the curve between
. This is equivalent to
approximating the area under the curve between 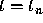 and
and 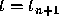 by the area of the shaded trapezoid. Further, we replace
by the area of the shaded trapezoid. Further, we replace 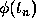 and
and
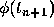 by their respective approximate values
by their respective approximate values 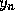 and
and 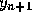 in this way we obtain from Eq. (11)
in this way we obtain from Eq. (11)
Since the unknown 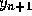 appears as one of the arguments of f on the
right side of Eq. (12), this equation defines
appears as one of the arguments of f on the
right side of Eq. (12), this equation defines 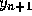 implicitly
rather than explicitly. Depending on the nature of the function f,
it may be fairly difficult to solve Eq. (12) for
implicitly
rather than explicitly. Depending on the nature of the function f,
it may be fairly difficult to solve Eq. (12) for 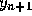 .
The difficulty can be overcome by replacing
.
The difficulty can be overcome by replacing 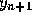 on the right side of
Eq. (12) by the value obtained using the Euler formula. Thus
on the right side of
Eq. (12) by the value obtained using the Euler formula. Thus
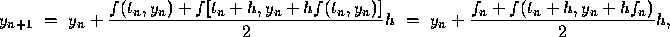
where 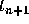 has been replaced by
has been replaced by 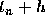 .
.
The above equation gives an explicit formula for computing 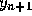 ,
the approximate value of
,
the approximate value of 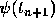 , in terms of the data at
, in terms of the data at 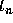 .
This formula is known as the improved Euler formula or the
Heun formula. The improved Euler formula is an example of a
two-stage method; that is, we first calculate
.
This formula is known as the improved Euler formula or the
Heun formula. The improved Euler formula is an example of a
two-stage method; that is, we first calculate 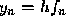 from the
Euler formula and then use this result to calculate
from the
Euler formula and then use this result to calculate 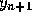 . The
local truncation error for the improved formula is
. The
local truncation error for the improved formula is 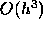 as opposed to
as opposed to
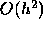 for the Euler's method. It can also be shown that for a finite
interval, the global truncation error for the improved Euler formula
is bounded by
for the Euler's method. It can also be shown that for a finite
interval, the global truncation error for the improved Euler formula
is bounded by 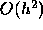 , so this method is a second order method. However, this
accuracy is achieved at the expense of more computational work.
, so this method is a second order method. However, this
accuracy is achieved at the expense of more computational work.
What happens when 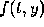 depends only on t andn not on y?
The differential equation
depends only on t andn not on y?
The differential equation 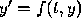 reduces to integrating
reduces to integrating 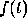 .
In this case, the improved Euler formula becomes
.
In this case, the improved Euler formula becomes
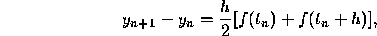
which is the trapezoid rule for numerical integration.


