Consider a unitary matrix 
,
where 
, 
. Therefore,
given any vector 
,
is symmetric,
is unitary,
is obtained by the reflection of
about the plane whose normal is 
,
.
Given 
, we want to find 
(and hence 
) such that 
is a multiple of the
first coordinate vector 
. Therefore,
With the requirement that 
, we obtain
Given 
, let 
be the
unitary matrix
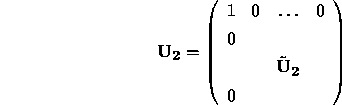
where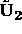 
is formed by the Householder
transformation for the column vector 
. Thus,
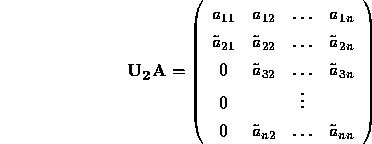
It is clear that 
does not change the first column of
. Repeating this procedure, 
is transformed by
orthogonal similarity transformations into an upper Hessenberg matrix.