QR Algorithm

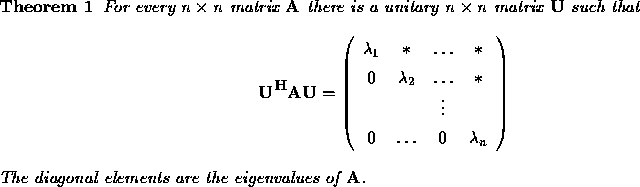
The basic QR algorithm to compute eigenvalues makes use of the Schur Normal Form. Schur's theorem states that

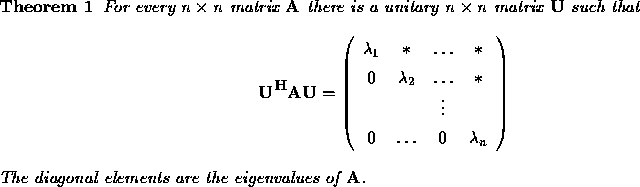
The basic QR algorithm can be written as follows:

 Given    ¯   ,
define   .

		 For    do

		 		 Calculate the QR decomposition   ,

		 		 Define   .

Computing the QR decomposition of a general matrix is computationally intensive ( operations) to perform at each step. To save this overhead, we use similarity transformations to convert to an upper Hessenberg matrix. Computing the QR decomposition of upper Hessenberg matrices is only an operation. It is important to note that the QR decomposition of an upper Hessenberg matrix yields an orthogonal component which also upper Hessenberg. Therefore, 's generated by the basic QR algorithm on upper Hessenberg matrices preserve the upper Hessenberg property.

• QR decomposition of upper Hessenberg matrices