Any matrix 
, has a QR factorization:
where 
has orthonormal columns and 
is upper triangular 
.
Every matrix has a unique 
factorization, which can
be computed using Gram-Schimdt orthogonalization. Read pages 134-137 of
Golub/Ortega for more details.
One way of computing the QR factorization is to pre-multiply 
by a sequence of Givens rotations---orthogonal matrices 
that
differ from the identity matrix only in a 
principal
submatrix, which has the form:
With 
a sequence of matrices 
satisfying
is generated. Each 
has one
more zero than the last, so 
= 
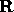, for 
To be specific, the zeros can be introduced in the order
; and so on. Check
out Golub/Ortega's book on the construction of the Givens matrix.