Let 
be a 
matrix, such that 
. Then we can
decompose it as:
where,
and
The columns of 
are the left singular vectors and the columns
of 
are the right singular vectors. The 
's are the
singular values. For a given matrix, the SVD is unique.
The smallest singular value 
is a good measure of whether the
given matrix is singular. A matrix is singular if 
.
The magnitude of 
is used to measure the ``nearness" to
singularity.
The eigenvalues of 
correspond to the square of the
singular values (
). As a result, the following relationships
can be derived:
If 
is a square matrix, than the SVD of 
is given
as 
. As a result, the singular
values of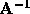 
are 
.
Moreover, 
.