Triangular systems play a fundamental role in matrix computations. Many methods are built on the idea of reducing a problem to the solution of one or more triangular systems. On serial computers triangular systems are universally solved by the standard back and forward substitution algorithms. We are going to perform backward error analysis on the substitution algorithms and show that these algorithms are extremely stable.
Given an an upper triangular matrix 
the
system
can be solved using the formula:
which yields the components of 
in order from last to first.
The resulting algorithm for back substitution looks like:
for 
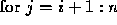
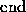
The analogous algorithm for solving a lower triangular system, forward substitution, is similar. To analyze the error in substitution we use the following lemma:
Lemma: Let 
be
evaluated in floating point arithmetic according to the following algorithm:
s = c
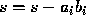
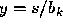
Then the computed 
satisfies
where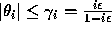 
and
is the machine precision.
This formulation of error bound has some useful properties. They are:
, in which the elements of 
are not perturbed.
terms are fairly tight in terms of
getting the best possible constants.
from the back substitution satisfies:
This results holds for the particular ordering of arithmetic operations
based on the algorithm highlighted above. For a general triangular
system, 
, where 
is an upper or lower
non-singular triangular matrix, solved by substitution, with any ordering.
Then the computed solution 
satisfies
