Poisson Resampling

Basic Poisson Resampling

The first technique we consider for introducing variability in the traffic generation process is Poisson Resampling. The starting point of every method presented in this chapter is a connection vector trace where is an augmented connection vector (an a-b-t connection vector plus some network-level parameters), and is its relative start time. The basic version of our Poisson Resampling technique consists of deriving a new trace by randomly choosing connection vectors from without replacement, and assigning them start times according to an exponential distribution. We define the duration of as , the length of the interval in which connections are started^7.1. Given a target duration for , the Poisson Resampling algorithm iteratively adds a new to until . Each is equal to some randomly selected , and

$$T_j^\prime = T_{j-1}^\prime+\delta_j,$$

where is sampled independently from an exponential distribution. The mean of this exponential distribution provides a way to control the density of connections in the derived trace. For example, if we intend to have the same density of connections in as in , we can compute the mean inter-arrival time of the connection vectors in , and use it as the mean of the experimental distribution used to construct . Given the light tail of the exponential distribution, the resulting number of connection vectors in is always very close to . If , the number of connection vectors in is also very close to .

Figure 7.1: Bodies of the distributions of connection inter-arrivals for UNC 1 PM and 1 AM, and their exponential fits.

Figure 7.2: Tails of the distributions of connection inter-arrivals for UNC 1 PM and 1 AM, and their exponential fits.

Figure 7.3: Bodies of the distributions of connection inter-arrivals for Abilene-I and Leipzig-II, and their exponential fits.

Figure 7.4: Tails of the distributions of connection inter-arrivals for Abilene-I and Leipzig-II, and their exponential fits.

The resampling technique described above has the advantage of its simplicity. Furthermore, it is statistically appealing, since the exponential distribution naturally arises from the combination of independent events. The use of connection inter-arrivals sampled independently from an exponential distribution is intuitively consistent with the view of traffic as a superposition of a large number of independent connections that transmit data through the same network link. Our empirical data, presented in Figures 7.1 to 7.4, confirm the applicability of this inter-arrival model. Figure 7.1 shows two pairs of CDFs comparing real connection arrivals and their exponential fits. The first pair (white symbols) corresponds to the distribution of connection inter-arrivals for UNC 1 PM (squares), and an exponential distribution^7.2 with the same mean (triangles). The second pair (black symbols) shows the distribution of connection inter-arrivals for UNC 1 AM and an exponential distribution with the same mean. Both fits are excellent, so exponentially distributed connection inter-arrivals are clearly a good starting point for a trace resampling technique. The tails of the empirical distributions, shown in Figure 7.2, are also consistent with the fitted exponentials. Their slope is slightly lower, which could motivate a fit with a more general distribution like Weibull. However, a small improvement in the fit would require an increase in the complexity of the model, since the one-parameter exponential model would have to be replaced by the two-parameter Weibull model. This additional effort would produce only a limited gain given that the exponential fit is excellent for 99.9% of the distribution.

Figures 7.3 and 7.4 consider another two traces, Abilene-I and Leipzig-II. The bodies are again very closely approximated, but the tails are heavier for the original data. Note that this effect is more pronounced as the traces get longer. The duration of the UNC traces is one hour, the duration of Abilene-I is 2 hours, and the duration of Leipzig-II is 2 hours and 45 minutes. This could suggest that the worse fit is due to non-stationarity in the connection arrival process, which becomes more likely for longer traces. Further analysis is needed to confirm this hypothesis or find an alternative explanation. We must note that these results are in sharp contrast with those in Feldmann [Fel00], where the empirical inter-arrival distributions were significantly different from the bodies^7.3 of fitted exponential distributions. The reason for this difference is unclear at this point^7.4.

Figure 7.5: Average offered load vs. number of connections for 1,000 Poisson resamplings of UNC 1 PM.

Figure 7.6: Histogram of the average offered loads in 1,000 Poisson resamplings of UNC 1 PM.

The main problem with the basic Poisson Resampling technique is the lack of control over the load offered by the replay of . As we will demonstrate, the number of connections in is only loosely correlated to the offered load. As a consequence, it becomes difficult to predict the load that a Poisson resampled trace generates, even for resamplings of the same duration and mean inter-arrival rate. This would force researchers to create many resampled traces until they hit upon a resampling with the intended offered load. We studied the wide range of offered loads that result from basic Poisson Resampling by performing a large of number of resamplings of the same connection vector trace .

As discussed in the introduction of this chapter, average load created by is equal to the total number of bytes in divided by its duration . Given that TCP headers and retransmitted segments usually represent only a small fraction of , the total size of the ADUs in divided by is also a close approximation of . We use this approximation to examine the average loads offered by a large number of Poisson resamplings, considering the offered load of a resampling equal to the total size of its ADUs divided by its duration . It is also important to note that the traces we consider are bidirectional, and they do not necessarily create the same average load in both directions. The analysis in the rest of this section will focus only on one direction of the trace, the target direction, whose average load is given the total size of the ADUs flowing in that direction divided by the duration of the trace. More formally, the total size of the ADUs in the target direction is equal to

$$s^\prime = \sum_{i\in C_{init}} \sum_{j=1}^{n_a^i} a_j^i + \sum_{i\in C_{acc}} \sum_{j=1}^{n_b^i} b_j^i,$$ (7.1)

where is the set of connection vectors in initiated in the target direction, is the rest of the connection in (the connections accepted rather than initiated in the target direction), and are the numbers of a-type and b-type ADUs of -th connection vector respectively, and and are the sizes of the -th a-type and b-type ADU of the -th connection vector respectively. Computing offered load as is only a convenient (and reasonable) approximation of the load generated by replaying . First, is an underestimation, since it does not take into account the total size of packet headers (only ADUs), and the retransmissions in the replay. Second, the duration of the replay of the connection vectors in will be somewhat above . only considers the period in which connections are started, but some of them will terminated after the last connection is started. An obvious example is the last connection. As we will demonstrate using experiments, the inaccuracy of is very small, so it provides a good foundation for understanding load scaling. This calculation is obviously much more convenient than replaying thousands of resamplings in the testbed network.

Figure 7.5 shows a scatterplot of the results of 1,000 resamplings of UNC 1 PM. The duration of the resamplings and their mean rate of connection inter-arrival were equal to the ones in UNC 1 PM. For each resampling, the total number of connections is shown on the x-axis, while the resulting offered load is shown on the y-axis. This plot demonstrates that basic Poisson Resampling results in traces with very small variability in the number of connection vectors, between 1,409,727 and 1,417,664 (the standard deviation was equal to 1,191.71). On the contrary, the range of offered loads is very wide, between 143.55 and 183.44 Mbps ( Mbps), centered around the offered load of , 161.89 Mbps. The distribution of offered loads and its spread is further illustrated by the histogram in Figure 7.6.

Figure 7.7: Tails of the distributions of connection sizes for UNC 1 PM.

Figure 7.8: Analysis of the accuracy of connection-driven Poisson Resampling from 6,000 resamplings of UNC 1 PM (1,000 for each target offered load).

The wide range of offered loads that can result from Poisson Resampling is due to the heavy-tailed nature of the distribution of the total number of bytes contributed by each connection vector. The tail of this distribution for the UNC 1 PM trace is shown in Figure 7.7. The values in the plot correspond to the target direction, i.e., for each connection in and 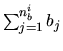for each connection in . The tails show non-negligible probabilities for very large sizes, and a linear decay of the probability over six orders of magnitude in the log-log CCDF. As a consequence, the contribution to the offered load made by each connection is highly variable and thus the number of connections in a trace is a poor predictor of its offered load. This makes basic Poisson Resampling inadequate for controlling load. Its only parameter is the mean inter-arrival rate of connections. This rate controls the same number of connections in the resampling, but not the total size of these connections, which varies greatly due to the heavy-tailed connection sizes. Figure 7.8 further illustrates this point using six sets of 1,000 trace resamplings, each set with a different target offered load. The plot shows a cross marking the mean of the load achieved by each of the sets of 1,000 experiments. The variability in the offered loads is illustrated using error bars for each set of experiments. The lower and upper endpoints of the error bars correspond to the 5th and 95th percentiles of the loads offered by each set of trace resamplings. Each set of trace resamplings had a fixed mean inter-arrival rate . Under the assumption that the mean offered load is proportional to the number of connections , we would expect the load to be inversely proportional to the mean arrival rate , since . Therefore, if the resamplings have the same duration , we would expect to achieve an offered load of

$$l^\prime = \frac{ l \mu^\prime } { \mu }$$ (7.2)

in each resampling. This expected value is shown in the x-axis as ``target offered load''. The mean of the loads offered by each set of resamplings is indeed equal to the expected (target) value. However, the error bars show a wide range of offered loads for the same , which is undesirable for a load scaling technique. For example, the width of the range of loads offered by the resamplings with the highest target load was 20 Mbps. Differences of this magnitude between resamplings can have a dramatic effect on the experiments, completely obscuring differences among competing mechanisms. The difficulty of precisely controlling the load using only the number of connections as a parameter motivated our refinement of Poisson Resampling to achieve far more predictable offered loads.

Byte-Driven Poisson Resampling

Figure 7.9: Comparison of average offered load vs. number of connections for 1,000 connection-driven Poisson resamplings and 1,000 byte-driven Poisson resamplings of UNC 1 PM.

Figure 7.10: Histogram of the average offered loads in 1,000 byte-driven Poisson resamplings of UNC 1 PM.

As the previous section demonstrated, the number of connection vectors in a trace is a poor predictor of the mean offered load achieved during the replay of a resampled trace . Therefore, controlling the number of connections in a resampling does not provide a good way of achieving a target offered load, and an alternative method is needed. In the idealized model of offered load in the previous section, the offered load was said to be exactly equal to . If so, we need to control the total number of bytes in the resampled trace to precisely match a target offered load. In Byte-driven Poisson Resampling, the mean inter-arrival rate of is not computed a priori using Equation 7.2. Instead, the target load is used to compute a target size for the payloads in the scaled direction.

Byte-driven Poisson Resampling has two steps:

1. We construct a set of connection vectors (without arrival times) by iteratively resampling the connection vectors in until the total payload size of the chosen connection vectors, computed using Equation 7.1, reaches .
2. We assign start times to the connection vectors in the resampling using the technique described in the previous section. The mean of the exponential distribution from which inter-arrival times are sampled is , where is the desired duration of , and is the number of connection vectors in the resampling.

Using this technique, and under the assumption that , the load offered by the resulting should be very close to the target load^7.5. Figure 7.9 demonstrates that this is the case by comparing the offered loads of 1,000 simulated trace resamplings constructed using the technique in section 7.1.1 and another 1,000 resamplings using the byte-driven technique. The target load of the byte-driven resamplings was 161.89 Mbps, which was the average load in the original UNC 1 PM trace. The range of achieved offered loads is far narrower for the second technique, thanks to the variable number of connection vectors that are assigned to each . The histogram in Figure 7.10 shows that the vast majority of the resamplings are very close to the target load ( Mbps).

Figure 7.11: Analysis of the accuracy of byte-driven Poisson Resampling from 4,000 resamplings of UNC 1 PM (1,000 for each target offered load).

Figure 7.11 summarizes the results of 4 sets of 1,000 byte-drive Poisson resamplings. The plot uses the same type of visualization found in Figure 7.8. The error bars, barely visible in this case, illustrate the accurate load scaling that can be achieved with Byte-driven Poisson Resampling.

Figure 7.12: Analysis of the accuracy of byte-driven Poisson Resampling using source-level traces replay: replays of three separate resamplings of UNC 1 PM for each target offered load, illustrating the scaling down of load from the original 177.36 Mbps.

Figure 7.13: Analysis of the accuracy of byte-driven Poisson Resampling using testbed experiments: replay of one resampling of UNC 1 AM for each target offered load, illustrating the scaling up of load from the original 91.65 Mbps.

The previous analysis demonstrated that accurate load scaling requires control of the total number of bytes in rather than of the total number of connections. This demonstration was based on the computation of the offered load using equation 7.1. It is important to verify that the actual load generated during a testbed replay of is similar to the computed load. To show that this is indeed the case, we replayed a number of resampled traces with four different target loads. Each resampled trace was then constructed using byte-driven Poisson Resampling, with a duration of 1 hour. To eliminate startup and shutdown effects, we only considered the middle 40 minutes for computing the achieved load. Figure 7.12 summarizes the results of the experiments for the resamplings of the UNC 1 PM trace. Each point corresponds to a separate replay experiment, showing the target load on the x-axis and the achieved load on the y-axis. We ran three experiments for each target load, and the results show a good approximation of the intended scaling line. Several experiments achieved loads a few Megabytes above the target. In general, we expected the experiments to have slightly higher achieved loads, since the scaling method focuses on the offered payload, ignoring packetization overhead (i.e., extra load from bytes in the packet headers). A more precise tuning of the offered load would take packetization into account, perhaps using a fixed constant to decrease the target payload, or by studying the total size (including headers) of each connection, as replayed in the same testbed environment. In any case, and given the above good results, it seems reasonable to ignore these further refinements.

The results in Figure 7.12 provide examples of scaling down the load of a trace, since the original load of UNC 1 PM was 177.36 Mbps, and 9 of the 12 experiments had target offered loads below this value. Scaling down the load of a trace using byte-driven resampling simply requires to choose a target load below the original load , which in turns means that the of the resampling will be below the original . These results confirm the close approximation of the target loads in the testbed experiments, where offered load is measured from real TCP segments (rather than computed using Equation 7.1). The plot shows for example that the three resamplings with target load 177.36 Mbps achieved loads of 176.72, 178.23 and 182.45 respectively. The impact of the TCP headers, retransmission and the slightly underestimated duration mentioned in the previous section is therefore very small. The results in Figure 7.13 provide an example of scaling up the load of a trace, since they correspond to byte-driven Poisson resamplings of UNC 1 AM, which had an original load of 91.65 Mbps. The resulting loads also approximate the intended targets very closely.