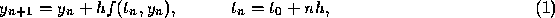
The use of numerical procedure, such as the Euler formula
to solve an initial value problem
raises a number of questions that must be answered before the approximate
numerical solution can be accepted as satisfactory.
One of these is the question of convergence. That is, as the step size
h tends to zero, do the values of the numerical solution
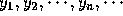approach the corresponding values of the
actual solution? Assuming that the answer is affirmative, there remains the
important practical question of how rapidly the numerical approximation
converges to the solution. In other words, how small a step size is needed
to guarantee a given level of accuracy? We want to use a step size
that is small enough to assure the required accuracy, but not too small.
An unnecessarily small step size slows down the calculations, makes them
more expensive, and in some cases may even cause a loss of accuracy.
