


Next: Improvements on the
Up: Errors in Numerical
Previous: Sources of Error
Let us assume that the solution 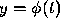 of the initial value problem
has a continuous second derivative in the interval of interest. To assure
this, we can assume that
of the initial value problem
has a continuous second derivative in the interval of interest. To assure
this, we can assume that 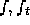 , and
, and  are continuous in the region
of interest. If f has these properties and if
are continuous in the region
of interest. If f has these properties and if 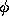 is a solution of the
initial value problem, then
is a solution of the
initial value problem, then

and by the chain rule
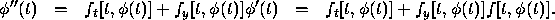
Since the right side of this equation is continuous, 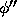 is also
continuous.
is also
continuous.
Then, making use of a Taylor polynomial with a remainder to expand 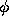 about
about 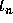 , we obtain
, we obtain
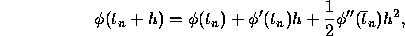
where 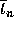 is some point in the interval
is some point in the interval 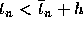 .
Subtracting Eq. (1) from this equation, and noting that
.
Subtracting Eq. (1) from this equation, and noting that
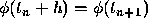 and
and
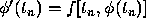 ,
we find that
,
we find that
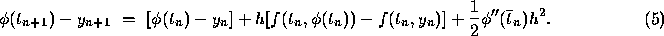
To compute the local truncation error we apply Eq. (5) to the true
solution 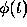 , that is, we take
, that is, we take 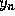 to be
to be 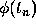 . Then we
immediately obtain from Eq. (5) that the local truncation error
. Then we
immediately obtain from Eq. (5) that the local truncation error
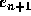 is
is
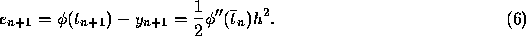
Thus the local truncation error for the Euler method is proportional
to the square of the step size h and the proportionality factor depends on
the second derivative of the solution 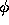 . The expression given by Eq.
(6) depends on n and, in general, is different for each step.
A uniform bound, valid on an interval [a, b], is given by
. The expression given by Eq.
(6) depends on n and, in general, is different for each step.
A uniform bound, valid on an interval [a, b], is given by

where M is the maximum of 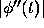 on the interval
on the interval 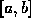 .
Since the equation given above is based on a consideration of the worst
possible case, that is, the largest possible value of
.
Since the equation given above is based on a consideration of the worst
possible case, that is, the largest possible value of 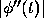 ,
it may well be a considerable overestimate of the actual local truncation
error in some parts of the interval
,
it may well be a considerable overestimate of the actual local truncation
error in some parts of the interval  . One use of Eq. (7) is
to choose a step size that will result in a local truncation error no greater
than some given tolerance level. For example, if the local truncation error
must be no greater than
. One use of Eq. (7) is
to choose a step size that will result in a local truncation error no greater
than some given tolerance level. For example, if the local truncation error
must be no greater than  , then from Eq. (7) we have
, then from Eq. (7) we have

The primary difficulty in using any of Eqs. (6), (7), or (8)
lies in estimating  or M. However, the central fact
expressed by these equations is that the local truncation error is proportional
to
or M. However, the central fact
expressed by these equations is that the local truncation error is proportional
to 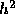 . Thus, if h is reduced by a factor of
. Thus, if h is reduced by a factor of 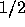 , then the error is
reduced by
, then the error is
reduced by 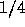 , and so forth.
In Golub/Ortega's book, it is mentioned that the local truncation error is
, and so forth.
In Golub/Ortega's book, it is mentioned that the local truncation error is
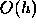 as opposed to
as opposed to 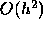 . It is because they implicitly divide it
by h. Their derivation of local trunctation error is based on the formula
. It is because they implicitly divide it
by h. Their derivation of local trunctation error is based on the formula
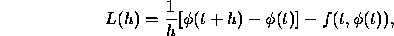
where 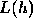 is the local truncation error.
is the local truncation error.
More important than the local truncation error is the global truncation
error 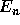 . The analysis for estimating
. The analysis for estimating 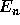 is more difficult than
that for
is more difficult than
that for 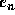 . However, knowing the local truncation error we can make
an intuitive estimate of the global truncation error at a fixed
. However, knowing the local truncation error we can make
an intuitive estimate of the global truncation error at a fixed
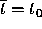 as follows. Suppose that we take n steps in going
from
as follows. Suppose that we take n steps in going
from 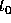 to
to 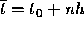 . In each step the error is at most
. In each step the error is at most
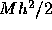 ; thus the error in n steps is at most
; thus the error in n steps is at most 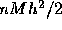 .
Noting that
.
Noting that 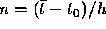 , we find that the global
truncation error for the Euler method in going from
, we find that the global
truncation error for the Euler method in going from
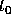 to
to 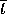 is bounded by
is bounded by

This argument is not complete since it does not take into account the effect
that an error at one step will have in succeeding steps. Nevertheless, it can
be shown that the global truncation error in using the Euler method on a
finite interval is no greater than a constant times h.
The Euler method is called a first order method because
its global truncation error is proportional to the first power of the step size.
Because it is more accessible, we will hereafter use the local truncation error as our principal measure of the accuracy of a numerical method, and
for comparing different methods. As an example of how we can use
the result (6) if we have a priori information about the
solution of the given initial value problem, consider the illustrative example.
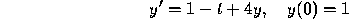
on the interval 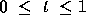 . Let
. Let 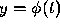 be the
solution of the initial value problem. Then, as noted previously,
be the
solution of the initial value problem. Then, as noted previously,
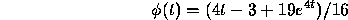
and therefore

Equation (6) then states that
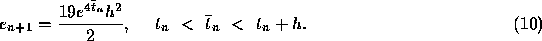
The appearance of the factor 19 and the rapid growth of 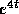 explain
why the results in the preceding section with
explain
why the results in the preceding section with 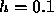 were not very accurate.
were not very accurate.
For example, the error in the first step is

It is clear that 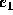 is positive and, since
is positive and, since 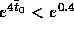 ,
we have
,
we have
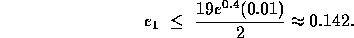
Note also that 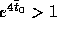 ; hence
; hence 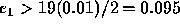 . The actual error is 0.1090418. It follows from Eq. (10) that
the error becomes progressively worse with increasing t;
Similar computations for bounds for the local truncation error give
. The actual error is 0.1090418. It follows from Eq. (10) that
the error becomes progressively worse with increasing t;
Similar computations for bounds for the local truncation error give
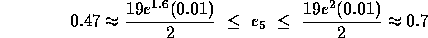
in going from 0.4 to 0.5 and
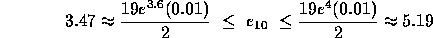
in going from 0.9 to 1.0.
These results indicate that for this problem the local truncation error
is about 40 or 50 times larger near t = 1 than near t = 0 .
Thus, to reduce the local truncation error to an acceptable level throughout
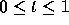 , one must choose a step size h based on an analysis near
t = 1. Of course, this step size will be smaller than necessary near
t = 0 . This results in more calculations than necessary, more time
consumed, and possibly more danger of unacceptable round-off errors.
Another approach is to keep the local truncation error approximately
constant throughout the interval by gradually reducing the step size as
t increases. In the example problem we would need to reduce h by a factor
of about seven in going from t = 0 to t = 1 . A method that provides
for variations in the step size is called adaptive. All modern
codes for solving differential equations have the capability of
adjusting the step size as needed. This includes the two routines ode23
and ode45 in Matlab.
, one must choose a step size h based on an analysis near
t = 1. Of course, this step size will be smaller than necessary near
t = 0 . This results in more calculations than necessary, more time
consumed, and possibly more danger of unacceptable round-off errors.
Another approach is to keep the local truncation error approximately
constant throughout the interval by gradually reducing the step size as
t increases. In the example problem we would need to reduce h by a factor
of about seven in going from t = 0 to t = 1 . A method that provides
for variations in the step size is called adaptive. All modern
codes for solving differential equations have the capability of
adjusting the step size as needed. This includes the two routines ode23
and ode45 in Matlab.



Next: Improvements on the
Up: Errors in Numerical
Previous: Sources of Error
Dinesh Manocha
Sun Mar 15 12:31:03 EST 1998
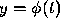 of the initial value problem
has a continuous second derivative in the interval of interest. To assure
this, we can assume that
of the initial value problem
has a continuous second derivative in the interval of interest. To assure
this, we can assume that 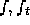 , and
, and  are continuous in the region
of interest. If f has these properties and if
are continuous in the region
of interest. If f has these properties and if 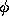 is a solution of the
initial value problem, then
is a solution of the
initial value problem, then




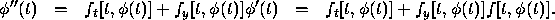
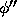 is also
continuous.
is also
continuous.
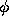 about
about 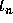 , we obtain
, we obtain
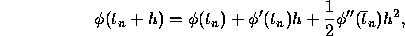
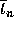 is some point in the interval
is some point in the interval 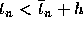 .
Subtracting Eq. (
.
Subtracting Eq. (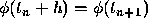 and
and
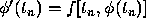 ,
we find that
,
we find that
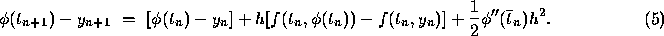
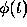 , that is, we take
, that is, we take 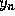 to be
to be 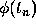 . Then we
immediately obtain from Eq. (
. Then we
immediately obtain from Eq. (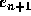 is
is
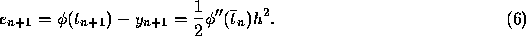
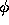 . The expression given by Eq.
(
. The expression given by Eq.
(
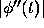 on the interval
on the interval 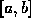 .
Since the equation given above is based on a consideration of the worst
possible case, that is, the largest possible value of
.
Since the equation given above is based on a consideration of the worst
possible case, that is, the largest possible value of 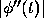 ,
it may well be a considerable overestimate of the actual local truncation
error in some parts of the interval
,
it may well be a considerable overestimate of the actual local truncation
error in some parts of the interval 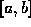 . One use of Eq. (
. One use of Eq. ( , then from Eq. (
, then from Eq. (
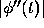 or M. However, the central fact
expressed by these equations is that the local truncation error is proportional
to
or M. However, the central fact
expressed by these equations is that the local truncation error is proportional
to 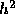 . Thus, if h is reduced by a factor of
. Thus, if h is reduced by a factor of 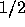 , then the error is
reduced by
, then the error is
reduced by 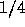 , and so forth.
In Golub/Ortega's book, it is mentioned that the local truncation error is
, and so forth.
In Golub/Ortega's book, it is mentioned that the local truncation error is
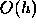 as opposed to
as opposed to 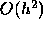 . It is because they implicitly divide it
by h. Their derivation of local trunctation error is based on the formula
. It is because they implicitly divide it
by h. Their derivation of local trunctation error is based on the formula
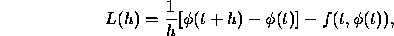
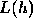 is the local truncation error.
is the local truncation error.
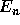 . The analysis for estimating
. The analysis for estimating 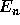 is more difficult than
that for
is more difficult than
that for 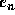 . However, knowing the local truncation error we can make
an intuitive estimate of the global truncation error at a fixed
. However, knowing the local truncation error we can make
an intuitive estimate of the global truncation error at a fixed
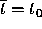 as follows. Suppose that we take n steps in going
from
as follows. Suppose that we take n steps in going
from 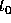 to
to 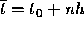 . In each step the error is at most
. In each step the error is at most
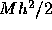 ; thus the error in n steps is at most
; thus the error in n steps is at most 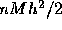 .
Noting that
.
Noting that 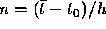 , we find that the global
truncation error for the Euler method in going from
, we find that the global
truncation error for the Euler method in going from
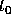 to
to 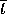 is bounded by
is bounded by

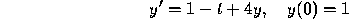
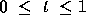 . Let
. Let 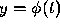 be the
solution of the initial value problem. Then, as noted previously,
be the
solution of the initial value problem. Then, as noted previously,
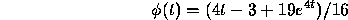

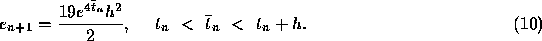
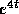 explain
why the results in the preceding section with
explain
why the results in the preceding section with 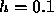 were not very accurate.
were not very accurate.

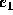 is positive and, since
is positive and, since 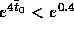 ,
we have
,
we have
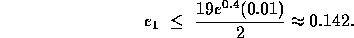
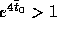 ; hence
; hence 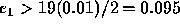 . The actual error is 0.1090418. It follows from Eq. (
. The actual error is 0.1090418. It follows from Eq. (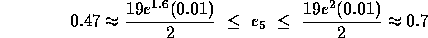
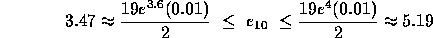
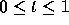 , one must choose a step size h based on an analysis near
t = 1. Of course, this step size will be smaller than necessary near
t = 0 . This results in more calculations than necessary, more time
consumed, and possibly more danger of unacceptable round-off errors.
Another approach is to keep the local truncation error approximately
constant throughout the interval by gradually reducing the step size as
t increases. In the example problem we would need to reduce h by a factor
of about seven in going from t = 0 to t = 1 . A method that provides
for variations in the step size is called adaptive. All modern
codes for solving differential equations have the capability of
adjusting the step size as needed. This includes the two routines ode23
and ode45 in Matlab.
, one must choose a step size h based on an analysis near
t = 1. Of course, this step size will be smaller than necessary near
t = 0 . This results in more calculations than necessary, more time
consumed, and possibly more danger of unacceptable round-off errors.
Another approach is to keep the local truncation error approximately
constant throughout the interval by gradually reducing the step size as
t increases. In the example problem we would need to reduce h by a factor
of about seven in going from t = 0 to t = 1 . A method that provides
for variations in the step size is called adaptive. All modern
codes for solving differential equations have the capability of
adjusting the step size as needed. This includes the two routines ode23
and ode45 in Matlab.