


Next: Three-Term Taylor Formula
Up: No Title
Previous: No Title
Earlier, we had mentioned the possibility of adjusting the
step size as a calculation proceeds so as to maintain the local truncation
error at a more or less constant level. The goal is to use no more steps than
necessary, and at the same time
to keep some control over the accuracy of the approximation. Here we will
describe how
this can be done. Suppose that after n steps we have reached the point
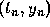 . We choose a step size h and calculate
. We choose a step size h and calculate 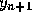 .
Next we need to estimate the error we have made in calculating
.
Next we need to estimate the error we have made in calculating 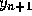 .
In the absence of knowing the actual solution the best that we can do is
to use a more accurate method and repeat the calculation starting from
.
In the absence of knowing the actual solution the best that we can do is
to use a more accurate method and repeat the calculation starting from
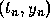 . For example, if we used the Euler method
for the original calculation, we might repeat with the improved Euler method.
Then the difference between the two calculated values is an estimate
. For example, if we used the Euler method
for the original calculation, we might repeat with the improved Euler method.
Then the difference between the two calculated values is an estimate
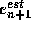 of the error in using the original method. If the estimated
error is different from the error tolerance
of the error in using the original method. If the estimated
error is different from the error tolerance  , then we adjust the
step size and repeat the calculation. The key to making this adjustment
efficiently is knowing how the local truncation error
, then we adjust the
step size and repeat the calculation. The key to making this adjustment
efficiently is knowing how the local truncation error 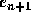 depends on the
step size h. For the Euler method the local truncation error is
proportional to
depends on the
step size h. For the Euler method the local truncation error is
proportional to 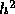 , so to bring the estimated error down
(or up) to the tolerance level
, so to bring the estimated error down
(or up) to the tolerance level  we might multiply the original step
size by the factor
we might multiply the original step
size by the factor 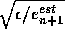 .
.
To illustrate this procedure consider the example problem,
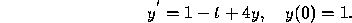
After one step with 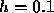 we obtain the values
we obtain the values 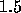 and
and 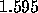 from the
Euler method and the improved Euler method, respectively.
Thus the estimated error in using the Euler method is
from the
Euler method and the improved Euler method, respectively.
Thus the estimated error in using the Euler method is 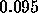 .
If we have chosen an error tolerance of
.
If we have chosen an error tolerance of 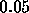 , for instance, then we need
to adjust the step size downward by the factor
, for instance, then we need
to adjust the step size downward by the factor 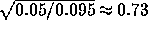 .
Rounding downward to be conservative, let us choose the adjusted step size
.
Rounding downward to be conservative, let us choose the adjusted step size
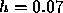 . Then, from the Euler formula we obtain
. Then, from the Euler formula we obtain
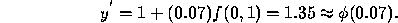
Using the improved Euler method we obtain 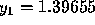 , so the estimated
error in using the Euler formula is
, so the estimated
error in using the Euler formula is 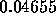 , which is slightly less than
the specified tolerance. The actual error, based on a comparison with the
solution itself, is somewhat greater, namely
, which is slightly less than
the specified tolerance. The actual error, based on a comparison with the
solution itself, is somewhat greater, namely 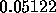 .
.
The same procedure can be followed at each step of the calculation, thereby
keeping the local truncation error approximately constant throughout the
entire numerical process. Modern adaptive codes for solving differential
equations adjust the step size as they proceed in very much this way, although
they usually use more accurate formulas than the Euler and improved Euler
formulas. Consequently, they are able to achieve both
efficiency and accuracy by using very small steps only where they are really
needed.



Next: Three-Term Taylor Formula
Up: No Title
Previous: No Title
Dinesh Manocha
Sun Mar 29 02:55:57 EST 1998
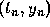 . We choose a step size h and calculate
. We choose a step size h and calculate 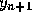 .
Next we need to estimate the error we have made in calculating
.
Next we need to estimate the error we have made in calculating 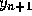 .
In the absence of knowing the actual solution the best that we can do is
to use a more accurate method and repeat the calculation starting from
.
In the absence of knowing the actual solution the best that we can do is
to use a more accurate method and repeat the calculation starting from
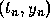 . For example, if we used the Euler method
for the original calculation, we might repeat with the improved Euler method.
Then the difference between the two calculated values is an estimate
. For example, if we used the Euler method
for the original calculation, we might repeat with the improved Euler method.
Then the difference between the two calculated values is an estimate
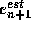 of the error in using the original method. If the estimated
error is different from the error tolerance
of the error in using the original method. If the estimated
error is different from the error tolerance  , then we adjust the
step size and repeat the calculation. The key to making this adjustment
efficiently is knowing how the local truncation error
, then we adjust the
step size and repeat the calculation. The key to making this adjustment
efficiently is knowing how the local truncation error 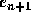 depends on the
step size h. For the Euler method the local truncation error is
proportional to
depends on the
step size h. For the Euler method the local truncation error is
proportional to 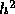 , so to bring the estimated error down
(or up) to the tolerance level
, so to bring the estimated error down
(or up) to the tolerance level  we might multiply the original step
size by the factor
we might multiply the original step
size by the factor 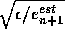 .
.



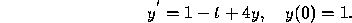
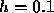 we obtain the values
we obtain the values 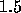 and
and 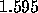 from the
Euler method and the improved Euler method, respectively.
Thus the estimated error in using the Euler method is
from the
Euler method and the improved Euler method, respectively.
Thus the estimated error in using the Euler method is 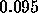 .
If we have chosen an error tolerance of
.
If we have chosen an error tolerance of 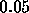 , for instance, then we need
to adjust the step size downward by the factor
, for instance, then we need
to adjust the step size downward by the factor 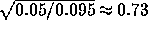 .
Rounding downward to be conservative, let us choose the adjusted step size
.
Rounding downward to be conservative, let us choose the adjusted step size
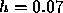 . Then, from the Euler formula we obtain
. Then, from the Euler formula we obtain
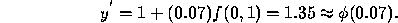
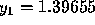 , so the estimated
error in using the Euler formula is
, so the estimated
error in using the Euler formula is 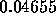 , which is slightly less than
the specified tolerance. The actual error, based on a comparison with the
solution itself, is somewhat greater, namely
, which is slightly less than
the specified tolerance. The actual error, based on a comparison with the
solution itself, is somewhat greater, namely 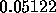 .
.