


Next: The Runge-Kutta Method
Up: No Title
Previous: Variation of Step
An alternative way of improving the Euler formula rests on the Taylor
expansion of the solution of the initial value problem. By retaining
the first two terms in the expansion of 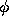 about
about 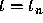 we obtain
the Euler formula, so by keeping more terms we should obtain a more accurate
formula. Assuming that f has continuous second partial derivatives, so that
we obtain
the Euler formula, so by keeping more terms we should obtain a more accurate
formula. Assuming that f has continuous second partial derivatives, so that
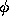 has at least three continuous derivatives in the interval of interest,
we can write
has at least three continuous derivatives in the interval of interest,
we can write
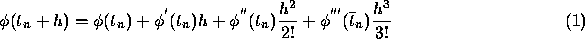
where  is some point in the interval
is some point in the interval 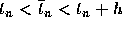 .
.
Since
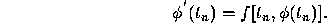
By differentiting this equation and then setting  we find that
we find that
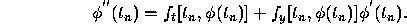
The three-term Taylor formula is obtained by replacing 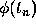 by its
approximate value
by its
approximate value 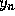 in the formulas for
in the formulas for 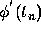 and
and
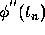 , and then neglecting the term
, and then neglecting the term 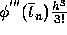 in Eq. (1). Thus we obtain
in Eq. (1). Thus we obtain
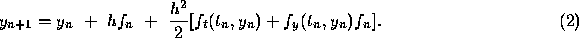
Assuming temporarily that 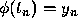 , it follows that the local
truncation error
, it follows that the local
truncation error 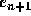 associated with formula (2) is
associated with formula (2) is
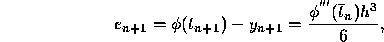
where 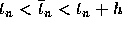 . Thus the local truncation error
for the three-term Taylor formula is proportional to
. Thus the local truncation error
for the three-term Taylor formula is proportional to  , just as
for the improved Euler formula discussed earlier. Again, it can also be shown
that for a finite interval the global truncation error is no greater than a
constant times
, just as
for the improved Euler formula discussed earlier. Again, it can also be shown
that for a finite interval the global truncation error is no greater than a
constant times 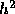 .
.
The three-term Taylor formula requires the computation of 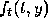 and
and
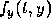 , and then the evaluation of these functions as well as
, and then the evaluation of these functions as well as
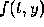 at
at 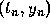 . In some problems
. In some problems 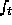 and
and 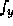 may be more
complicated than f itself. If this is the case, it is probably better to
use a formula with comparable accuracy, such as the improved Euler formula,
that does not require the partial derivatives
may be more
complicated than f itself. If this is the case, it is probably better to
use a formula with comparable accuracy, such as the improved Euler formula,
that does not require the partial derivatives 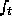 and
and 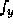 .
In principle, four-term or higher order Taylor formulas can be developed.
However, such formulas involve even higher partial derivatives of f and are
in general rather awkward to use.
.
In principle, four-term or higher order Taylor formulas can be developed.
However, such formulas involve even higher partial derivatives of f and are
in general rather awkward to use.
Finally, we note that if f is linear in both t and y, as in problem in
the example we have been using, then the improved Euler and three-term Taylor
formulas are identical.



Next: The Runge-Kutta Method
Up: No Title
Previous: Variation of Step
Dinesh Manocha
Sun Mar 29 02:55:57 EST 1998
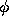 about
about 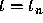 we obtain
the Euler formula, so by keeping more terms we should obtain a more accurate
formula. Assuming that f has continuous second partial derivatives, so that
we obtain
the Euler formula, so by keeping more terms we should obtain a more accurate
formula. Assuming that f has continuous second partial derivatives, so that
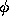 has at least three continuous derivatives in the interval of interest,
we can write
has at least three continuous derivatives in the interval of interest,
we can write



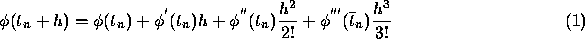
 is some point in the interval
is some point in the interval 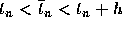 .
.
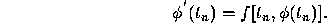
 we find that
we find that
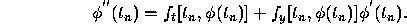
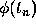 by its
approximate value
by its
approximate value 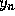 in the formulas for
in the formulas for 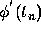 and
and
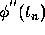 , and then neglecting the term
, and then neglecting the term 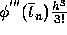 in Eq. (
in Eq. (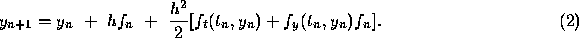
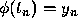 , it follows that the local
truncation error
, it follows that the local
truncation error 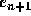 associated with formula (
associated with formula (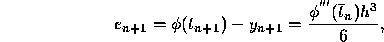
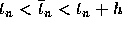 . Thus the local truncation error
for the three-term Taylor formula is proportional to
. Thus the local truncation error
for the three-term Taylor formula is proportional to  , just as
for the improved Euler formula discussed earlier. Again, it can also be shown
that for a finite interval the global truncation error is no greater than a
constant times
, just as
for the improved Euler formula discussed earlier. Again, it can also be shown
that for a finite interval the global truncation error is no greater than a
constant times 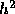 .
.
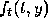 and
and
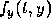 , and then the evaluation of these functions as well as
, and then the evaluation of these functions as well as
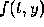 at
at 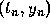 . In some problems
. In some problems 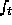 and
and 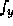 may be more
complicated than f itself. If this is the case, it is probably better to
use a formula with comparable accuracy, such as the improved Euler formula,
that does not require the partial derivatives
may be more
complicated than f itself. If this is the case, it is probably better to
use a formula with comparable accuracy, such as the improved Euler formula,
that does not require the partial derivatives 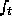 and
and 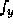 .
In principle, four-term or higher order Taylor formulas can be developed.
However, such formulas involve even higher partial derivatives of f and are
in general rather awkward to use.
.
In principle, four-term or higher order Taylor formulas can be developed.
However, such formulas involve even higher partial derivatives of f and are
in general rather awkward to use.