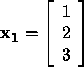 in meters and
in meters and
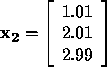 in meters. Then
in meters. Then  is a good approximation to
is a good approximation to  because the rel. error
because the rel. error
We use norms for error analysis. The natural question arises: which norm should we use?
Example: Given 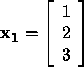 in meters and
in meters and
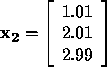 in meters. Then
in meters. Then  is a good approximation to
is a good approximation to  because the rel. error
because the rel. error
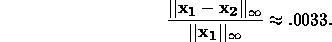
And 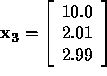 is considered a bad approximation as
is considered a bad approximation as

But suppose the first component of each vector is measured in kms. In this case,
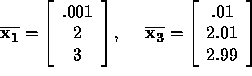 . The relative error measured
as:
. The relative error measured
as:

If we use a different norm, say the 1-norm, the results would be different.
Definiton: Let B be real linear space,
 :
:
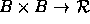 is an inner product if
is an inner product if
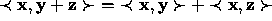
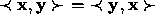
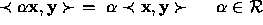
 if
if  .
.
Example: Over 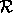 ,
, 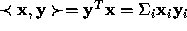
Lemma: Cauchy-Schwartz:  .
.
Lemma: 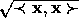 is a norm.
is a norm.
Definition: 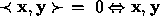 are orthogonal.
are orthogonal.
Lemma: Let 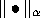 and
and 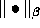 be two norms on
be two norms on 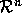 , then
, then
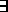 constants
constants 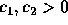 such that
such that
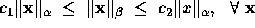 .
.
For some particular norms, the following results are useful:
