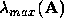is a matrix norm on
is a matrix norm on
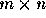 matrices if it is a vector norm on an
matrices if it is a vector norm on an 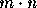 dimensional
space:
dimensional
space:
Definition:  is a matrix norm on
is a matrix norm on
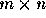 matrices if it is a vector norm on an
matrices if it is a vector norm on an 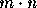 dimensional
space:
dimensional
space:
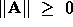 , and
, and 
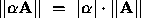
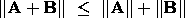
Definition: Let
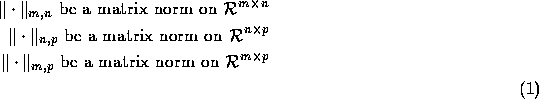
They are called mutually consistent if 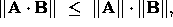
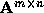 ,
, 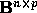
Example: 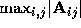 is the ``max norm".
is the ``max norm".
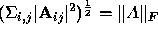 , is the
Frobenius norm.
, is the
Frobenius norm.
Definition: Given 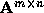 , let
, let 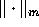 be a vector norm on
be a vector norm on 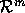 ,
, 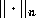 be a vector norm on
be a vector norm on
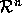 . Then
. Then
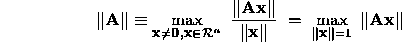
is called an operator norm or induced norm. The geometric interpretation of
such a norm is that it is the maximum length of a unit vector after
transformation by 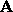 . Furthermore, an operator norm is a matrix norm
(i.e. satisfies the property listed above).
. Furthermore, an operator norm is a matrix norm
(i.e. satisfies the property listed above).
Definition: A real square matrix 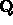 is orthogonal,
if
is orthogonal,
if 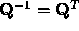 . For an orthogonal matrix, all the rows
and columns have
. For an orthogonal matrix, all the rows
and columns have 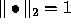 and are orthogonal to one another.
and are orthogonal to one another.
Some properties of matrix and vector norms:
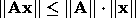 for operator and (Frobenius norm + vector 2 norm)
for operator and (Frobenius norm + vector 2 norm)
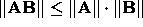 for
operator and Froberiur norm.
for
operator and Froberiur norm.
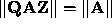 if
if 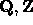 are
orthogonal for Frobenius and operator norm induced by
are
orthogonal for Frobenius and operator norm induced by  .
.
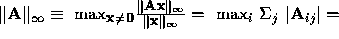 max absolute row sum.
max absolute row sum.
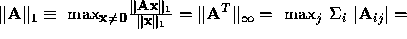 max absolute column sum.
max absolute column sum.
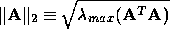 ,
where
,
where 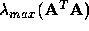 is the absolute value of the largest
eigenvalue in magnitude of the matrix
is the absolute value of the largest
eigenvalue in magnitude of the matrix 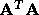 . (This
. (This 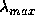 is called the spectral radius of the matrix.) If
is called the spectral radius of the matrix.) If 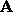 is symmetric,
is symmetric,
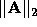 corresponds to the maximum absolute eigenvalue, i.e.
corresponds to the maximum absolute eigenvalue, i.e.