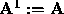 ,
,
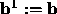 , and finishing with the upper triangular system
, and finishing with the upper triangular system
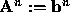 .
.



The strategy of GE is to reduce a problem that we can't solve (a full linear
system) to one that we can (a triangular system), using elementary row
operations. There are n-1 stages, begining with 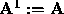 ,
,
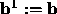 , and finishing with the upper triangular system
, and finishing with the upper triangular system
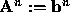 .
.
At the kth stage we have converted the original system to 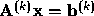 , where
, where
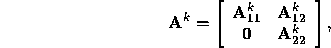
with 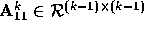 upper triangular.
The purpose of the kth stage of the elimination is to zero the elements
below the diagonal in the kth column of
upper triangular.
The purpose of the kth stage of the elimination is to zero the elements
below the diagonal in the kth column of 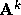 . This is accomplished
by the operations
. This is accomplished
by the operations
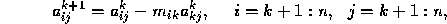
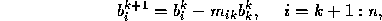
where the multipliers 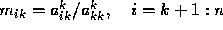 . At the
end of the
. At the
end of the  st stage we have the upper triangular system
st stage we have the upper triangular system
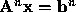 , which is solved by back substitution.
For an
, which is solved by back substitution.
For an 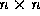 matrix, GE requires
matrix, GE requires 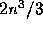 flops.
flops.
There are two problems with the method described above. They are:
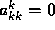 .
.
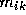 is
large, then there is a possible loss of significance: in the subtraction
is
large, then there is a possible loss of significance: in the subtraction
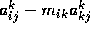 , low-order digits of
, low-order digits of 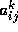 could be lost.
Losing these digits could correspond to making a relatively large change to
the original matrix
could be lost.
Losing these digits could correspond to making a relatively large change to
the original matrix 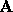 . The simplest example of this phenomenan is
for the matrix:
. The simplest example of this phenomenan is
for the matrix:

In this case, 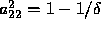 , and
, and 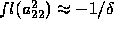 ,
if
,
if  (machine-precision), which would be the exact answer if
we changed
(machine-precision), which would be the exact answer if
we changed
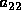 from 1 to 0. In this case, the matrix
from 1 to 0. In this case, the matrix 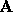 is
very well conditioned. The problem, of course, is with the choice of
is
very well conditioned. The problem, of course, is with the choice of
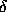 as the pivot.
as the pivot.
This problem can be solved by use of partial or complete pivoting. In partial pivoting, at the start of the kth stage, the kth and rth rows are interchanged, where
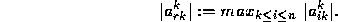
Partial pivoting ensures that the multipliers are nicely bounded:
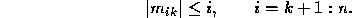
A more expensive pivoting strategy, which interchanges both rows and columns is complete pivoting. At the start of the kth stage, rows k and r and columns k and s are inter-changed, where
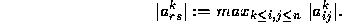
This requires 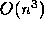 comparisons in total, compared with
comparisons in total, compared with 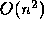 for
partial pivoting. Because of the searching overhead, and because partial
pivoting works so well, complete pivoting is rarely used in practice.
for
partial pivoting. Because of the searching overhead, and because partial
pivoting works so well, complete pivoting is rarely used in practice.


