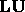 factorization of
factorization of 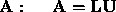 ,
where
,
where 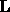 is unit lower triangular and
is unit lower triangular and  is upper triangular.
is upper triangular.



GE computes an 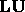 factorization of
factorization of 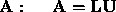 ,
where
,
where 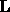 is unit lower triangular and
is unit lower triangular and  is upper triangular.
is upper triangular.
Theorem: There exists a unique 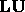 factorization
of
factorization
of 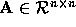 if and only if
if and only if 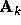 is
non-singular for
is
non-singular for 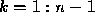 . If
. If 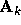 is singular for some
is singular for some
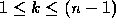 then the factorization may exist, but if so it
is not unique.
then the factorization may exist, but if so it
is not unique.
Proof: By induction (from Golub and Van Loan, 1992).
The effect of partial or complete pivoting is equivalent to multiplying
the matrix by a permuation matrix 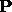 . GE with partial pivoting (GEPP)
applied to
. GE with partial pivoting (GEPP)
applied to  is equivalent to GE without pivoting applied to the
row-permuted matrix
is equivalent to GE without pivoting applied to the
row-permuted matrix 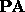 . This holds for all n: GEPP computes a
factorization
. This holds for all n: GEPP computes a
factorization 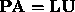 .
.
Computing an  factorization is equivalent to solving the
equations:
factorization is equivalent to solving the
equations:
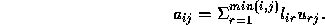
If these non-linear equations are examined in the right order, they can be
easily solved. For added generality let
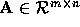 ,
, 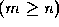 , and consider an
, and consider an
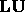 factorization with
factorization with 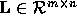 and
and 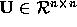 (
(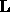 is lower
triangular). Suppose we know the first k - 1 columns of
is lower
triangular). Suppose we know the first k - 1 columns of 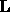 and the
first k - 1 rows of
and the
first k - 1 rows of  . Setting
. Setting 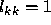 ,
,
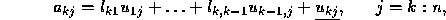

We can solve for the underlined elements in the kth row of  and
then the kth column of
and
then the kth column of  . This process is called Doolittle's
method. It computes the
. This process is called Doolittle's
method. It computes the 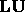 factorization, assuming that the
factorization exists.
factorization, assuming that the
factorization exists.
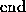
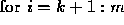
Cost: 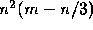 flops.
flops.
Doolittle's method is mathematically equivalent to GE without pivoting, for we have,
Doolittle's method is well suited to calculations by hand or with a desk
calculator, because it obviates the need to store the intermediate
quantities 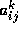 . It is also attractive when we can accumulate inner
products in extended precision. It is straightforward to incorporate partial
pivoting into Doolittle's method. However, complete pivoting cannot be
incorporated without changing the method.
. It is also attractive when we can accumulate inner
products in extended precision. It is straightforward to incorporate partial
pivoting into Doolittle's method. However, complete pivoting cannot be
incorporated without changing the method.


