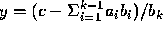The error analysis of GE is a combination of the error analysis of inner products and substitution. All mathematically equivalent variants of GE satisfy a common error bound. This is based on the connection between standard GE and Doolittle's methods, as shown in (3). Whether the inner product in (3) is calculated as one operation, or whether its terms are calculated many operations apart, precisely the same rounding errors are sustained (assuming that the extended precision accumulation of inner products is not used); all that changes is the moment when those rounding errors are committed.
It suffices, then, to analyze Doolittle's method. It also suffices to
analyze the method without pivoting, because GE with partial or complete
pivoting is equivalent to GE without pivoting applied to a permuted
matrix. The assignments in the Doolittle algorithm, corresponding to
(1) and (2) are of the form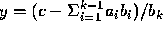 
.
After some algebraic manipulations, it can be shown that the computed
matrices 
and 
satisfy the bound:
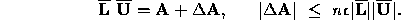
where, given a matrix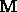 
, 
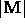represents a matrix with non-negative
entries obtained by taking the absolute value of every entry of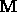 
.
Theorem: Let
where 
and
suppose GE produces computed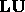 
factors, 
,
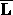, and a computed solution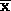 
to
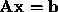, Then
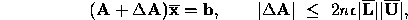
is the machine precision.
How do we interpret this theorem? We would like very much that the entries
of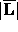 
and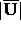 
are small. Ideally,
we would like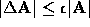 
, which corresponds
to the uncertainty introduced by rounding the elements of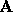 
. However,
because each element of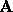 
undergoes up to n arithmetic operations,
we cannot expect better than a bound
of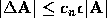 
, where 
.
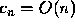Such a bound holds if 
and 
satisfy
which certainly holds if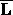 
and 
are
nonnegative. That is one class of matrices.
Based on these results, it is easy to see that the stability of GE is
determined not by the size of the multipliers but by the size of the matrix
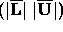. This matrix can be small when
the multipliers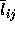 
are large, and large when the
multipliers are of order 1.
To understand the stability of GE further, we turn to norms (as will be the case in Homework 3). For GE without pivoting, the ratio
can be arbitrarily large. For example, for the matrix
the ratio is of order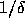 
.
Assume that partial pivoting is
used. Then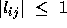 
for all 
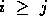, since the
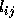are the multipliers. Moreover, it is easy to show by induction
that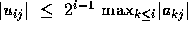 
.
Hence, for partial pivoting,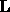 
is small and 
is bounded
relative to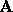 
.
The backward error analysis for GE is expressed in terms of the growth factor
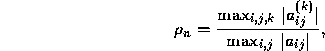
which involves all the elements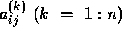 
that occur
during the elimination. It is easy to show that the growth factor satisfies
the following bound:
for partial pivoting. There exists class of matrices for which this bound is a tight bound.