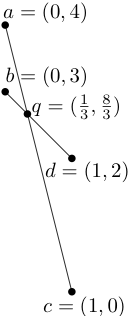We usually think of computers as good at mathematical calculations but, in fact, they often allow a small amount of error so that they can go fast: 1/3 might be stored as just the first 16 digits of 0.3333…, , so that 3*(1/3) < 1. This can cause problems when numerical calculations are used to figure out geometric relationships: rounding the coordinates of the point q actually takes it off the lines ac and bd that define it!

You can sometimes see this in video games – your character might be able to put a hand inside a wall because the computer is allowing a small error. And while you may enjoy the possibility to “cheat” in a video game, you would not want the software in an airplane or a surgical robot to violate the laws of nature in this way. Yet most techniques to avoid these errors require special programming and slow down both the development and execution of computer programs.

Algorithm designers try to minimize use of resources of time and memory space. Our work considers arithmetic precision as another resource, and minimizes the degree of polynomials used in the geometric tests or predicates that are applied.

For example, consider the problem of overlaying maps of roads and county boundaries. If the input is 2D points with b bit coordinates, then testing if two line segments intersect is degree 2 (double precision) but actually computing the intersection is a rational polynomial with degree 3 over degree 2. Some algorithms that compute intersections also sort them by x-coordinate, which takes degree 5, or five-fold precision. (Since computer hard-ware usually provides fast double precision only, it is not surprising that occasional errors occur when you need quintuple precision!)

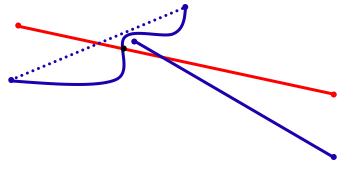
Developing fast algorithms with limited precision requires creativity. If you restrict yourself to degree two, you can determine whether two lines intersect, but you learn very little about where the intersection actually occurs.

Treating precision as a limited resource brings to our attention the high cost of sophisticated geometric operations. Moreover, it allows us to better guarantee that implementations of our algorithms are not only efficient, but also correct.