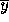 to
to 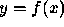 is computed
in an arithmetic of precision
is computed
in an arithmetic of precision  , where f is a real scalar
function of a real scalar variable. How should we measure the
``quality" of
, where f is a real scalar
function of a real scalar variable. How should we measure the
``quality" of 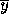 ?
?
Suppose that an approximation 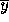 to
to 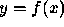 is computed
in an arithmetic of precision
is computed
in an arithmetic of precision  , where f is a real scalar
function of a real scalar variable. How should we measure the
``quality" of
, where f is a real scalar
function of a real scalar variable. How should we measure the
``quality" of 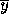 ?
?
In many cases, we would be happy with a tiny relative error, 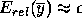 , but this cannot always be achieved. Instead of
focusing on the relative error of
, but this cannot always be achieved. Instead of
focusing on the relative error of 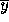 we can ask ``for what
set of data have we actually solved our problem?", that is, for what
we can ask ``for what
set of data have we actually solved our problem?", that is, for what 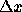 do we have
do we have 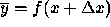 ? In general, there may be
many such
? In general, there may be
many such 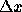 , so we should ask for the smallest one. The value
of
, so we should ask for the smallest one. The value
of 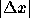 , possibly divided by |x|, is called the
backward error. The absolute and relative errors of
, possibly divided by |x|, is called the
backward error. The absolute and relative errors of 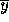 are
called forward errors. Figure 3 highlights the relationship
between these errors.
are
called forward errors. Figure 3 highlights the relationship
between these errors.
The process of bounding the backward error of a computed solution is called backward error analysis. It interprets rounding errors as being equivalent to perturbations in the data. The data frequently contains uncertainties due to previous computations or errors committed in storing numbers on the computer. If the backward error is no larger than these uncertainties then the computed solution can hardly be criticized.
A method for computing 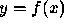 is called backward stable if,
for any x, it produces a computed
is called backward stable if,
for any x, it produces a computed 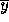 with a small backward
error, that is,
with a small backward
error, that is, 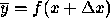 for some small
for some small
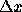 . The definition of ``small" is context dependent. Many
a times we use
. The definition of ``small" is context dependent. Many
a times we use 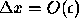 , where
, where  is the
machine epsilon.
is the
machine epsilon.