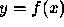 example, let an approximate solution
example, let an approximate solution 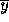 satisfy
satisfy
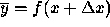 . Then, assuming that f is twice
differentiable,
. Then, assuming that f is twice
differentiable,
The relationship between forward and backward error for a problem
is governed by the conditioning of the problem, that is, the
sensitivity of the solution to the perturbations in the data. Using
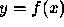 example, let an approximate solution
example, let an approximate solution 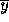 satisfy
satisfy
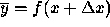 . Then, assuming that f is twice
differentiable,
. Then, assuming that f is twice
differentiable,
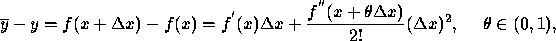
and we can bound or estimate the right hand side. This expansion leads to the notion of condition number. Since
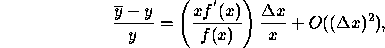
the quantity

measures, for small 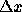 , the relative change in the output for a
given relative change in the input, and it is called the condition
number of f. If x or f is a vector then the condition number is
defined in a similar way using norms (we will cover them later in the
course) and it measures the maximum relative change.
In general, the forward error, backward error and the condition number
satisfy the following rule:
, the relative change in the output for a
given relative change in the input, and it is called the condition
number of f. If x or f is a vector then the condition number is
defined in a similar way using norms (we will cover them later in the
course) and it measures the maximum relative change.
In general, the forward error, backward error and the condition number
satisfy the following rule:
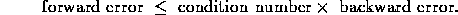
The condition number of a problem is always greater than or equal to one. A problem is ill-conditioned if its condition number is high. It is ill-posed if its condition number is very high (say infinity).