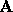In many applications, such as solving boundary value differential equations and sparse optimizations, the resulting matrices have a special structure. In such cases, we want to exploit that structure to improve the overall speed, accuracy and storage (as opposed to using Gaussian elimination on a dense matrix). The class of matrices include:
Remember, that a matrix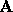 
is s.p.d. if
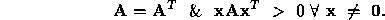
It is know that if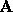 
is s.p.d.
than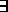 
a lower triangular non-singular matrix
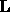, such that 
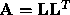. This decomposition
is called the Cholesky Factorization.
Therefore,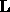 
can overwrite the
lower half of 
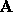. The total storage needed for
the output of Gaussian elimination is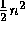 
.
Operation Count: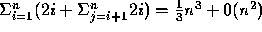 
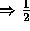work of GE (for general non-symmetric matrices).