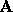 be a band matrix
with bandwidth KL and KU. Let
be a band matrix
with bandwidth KL and KU. Let 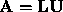 be its
LU decompositin (computed without pivoting). Then
be its
LU decompositin (computed without pivoting). Then 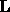 has lower
bandwidth KL and
has lower
bandwidth KL and  has upper bandwidth KU.
has upper bandwidth KU.



Band matrices are a special type of sparse matrix, where only the elements along the main diagonal and sub-diagonals are non-zero. Normally we use the symbols KL to represent the lower semi bandwidth and KU to represent the upper semi bandwidth (as shown in Figure 1).
They come from discretizing problems on meshes with near neighbour interaction. In particular, solutions of partial differential equations and boundary value problems result in band matrices.
Property: Let 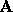 be a band matrix
with bandwidth KL and KU. Let
be a band matrix
with bandwidth KL and KU. Let 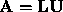 be its
LU decompositin (computed without pivoting). Then
be its
LU decompositin (computed without pivoting). Then 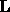 has lower
bandwidth KL and
has lower
bandwidth KL and  has upper bandwidth KU.
has upper bandwidth KU.
It can be computed at cost 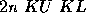 ,
where KU and KL are typically small compared to n.
,
where KU and KL are typically small compared to n.
space = 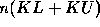 .
.
The full cost of solving 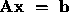 is
is 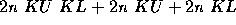 .
.