Beyond Comparing Connection Vectors

The main goal of this dissertation is to improve the state-of-the-art in closed-loop traffic generation by developing a better approach to source-level modeling. In particular, we presented in Chapter 3 the sequential and concurrent versions of the a-b-t model, which provide a first method for describing source-level behavior in an application-independent manner. We also discussed an efficient data acquisition algorithm for extracting a-b-t connection vectors from the packet headers of TCP connections. The first way in which we justified our source-level model was by examining connections from different applications, and demonstrating that their source-level descriptions in terms of a-b-t connection vectors properly captured their source-level behavior. The second way in which we can justify the model is to study the traffic generated using this model. If generated traffic is shown to closely approximate original traffic, this would strongly support the claim that the a-b-t model is a good description of source behavior. In other words, given that the statistical characteristics of are obviously a function of source behavior, being able to generate a statistically similar to would confirm the quality of as a description of the original source behavior.

Comparing and is however a subtle exercise. The actual replay of necessarily requires choosing a set of network-level parameters, such as round-trip times and TCP receiver window sizes, for each TCP connection in the source-level trace replay experiment. The exact set of packets and their arrival times is a direct function of these parameters, as explained in Chapter 4. As a consequence, if we were to conduct a source-level trace replay using arbitrary network-level parameters, we would obtain a with little resemblance to the original . The replayed a-b-t connection vectors may be a perfect description of the source behavior driving the original connections, but the generated would still be very different from the original . To address this difficulty, the replay should incorporate network-level parameters individually derived from for each connection. In Chapter 4, we described and evaluated methods for measuring three important network-level parameters: round-trip time, TCP receiver window size and loss rate. While this set of parameters is by no means complete, it does include the main parameters that affect the average throughput of a TCP connection, [PFTK98]. In this chapter, we examine the results of several source-level trace replay experiments, showing that the generated traffic is remarkably close to the original traffic. This is a strong justification of our source-level modeling approach, since it demonstrates that the closed-loop replay of a-b-t connection vectors provides a good approximation of the original traffic.

Incorporating network-level properties is important, but it is critical to understand the main shortcoming of this approach. The goal of our work is not to make the generated traffic identical to the original traffic , which could be accomplished with a simple packet-level replay. The goal is to develop a closed-loop traffic generation method based on a rich characterization of source behavior. Comparing and is a means to understand the quality of traffic generation method, where quality is considered to be higher as the original trace is more closely approximated. By construction, traffic generated using source-level trace replay can never be identical to the original traffic. The statistical properties of original packet header traces are the result of multiplexing a large number of connections into a single link, and these connections traverse a large number of different paths with a variety of network conditions. It is simply not possible to fully characterize this environment and reproduce it in a laboratory testbed or in a simulation. This is both because of the limitations of passive inference from packet headers, and because of the stochastic nature of network traffic. Source-level trace replay can never incorporate every factor that shaped , and therefore differences between and are unavoidable. Still, finding a close match between an original trace and its replay, even if they are not identical, constitutes strong evidence in favor of our a-b-t model and our data acquisition and generation methods. It also demonstrates the feasibility of generating realistic network traffic in a closed-loop manner that resembles a rich traffic mix.

Besides evaluating source-level trace replay by comparing original traces and their replays, this chapter also considers whether detailed source-level modeling is necessary to achieve high-quality traffic generation. This is accomplished by comparing traffic generated using (i.e., replaying connection vectors and network-level parameters) and traffic generated using a simplified version of with collapsed epochs, which we will name . Formally, given a sequential connection vector , with epoch tuples of the form , we define the version of with collapsed epochs as

$$C_i^{coll}=((\sum_{i=1}^n a_i, 0, \sum_{i=1}^n b_i, 0)).$$

The only a-type ADU size in the resulting connection vector is the total amount of data sent from the connection initiator to the connection acceptor, and the only b-type ADU size is the total amount of data sent from the connection acceptor to the connection initiator. No quiet time is part of a connection vector after collapsing its epochs. Similarly, given a concurrent connection vector , where

$$\alpha = ((a_1, ta_1), (a_2, ta_2), \dots, (a_{n_a}, ta_{n_a}))$$

and

$$\beta = ((b_1, tb_1), (b_2, tb_2), \dots, (b_{n_b}, tb_{n_b})),$$

we define the version of with collapsed epochs as

$$C^{coll}_k=((\sum_{i=1}^{n_a} a_i,0), (\sum_{i=1}^{n_b} b_i,0)).$$

Traffic generated according to does not incorporate any internal source-level structure of connections, i.e., epochs and inter-ADU quiet times are ignored. For this reason, we say that the collapsing of epochs ``removes'' detailed source-level modeling. Note however that even if epochs are collapsed, the total amount of data transferred in each direction does not change. The results in this chapter demonstrate that traffic generated using is substantially closer to the original traffic than traffic generated using .

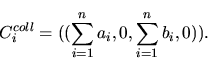
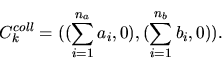
The evaluation of source-level trace replay presented in this chapter examines the results of replaying five traces. These traces were first considered in Section 3.5: Leipzig-II, UNC 1 PM, UNC 1 AM, UNC 7:30 PM and Abilene-I. Our analysis compares the statistical characteristics of each of these traces and their replays using the following metrics:

• time series of byte throughput,
• time series of packet throughput,
• Body and tail of the marginal distribution of byte throughput,
• Body and tail of the marginal distribution of packet throughput,
• Wavelet spectrum (logscale diagram),
• Estimated Hurst parameter and its confidence interval, and
• time series of the number of active connections.

These metrics were introduced in Section 4.2. For each original trace, we compare four different replays, conducted using tmix and usernet in the testbed shown in Figure 5.2. The first replay is the lossless replay, which replayed the a-b-t connection vectors in , giving each TCP connection its measured round-trip time and TCP receiver window sizes. The second replay is the lossy replay, which was identical to the first one, but it also applied random packet dropping to each TCP connection according to its measured loss rate. The third replay, is the lossless replay with collapsed epochs, which replayed the a-b-t connection vectors after they had their epochs collapsed, and it also gave each connection its measured round-trip time and TCP received window sizes. The fourth replay is the lossy replay with collapsed epochs, which was identical to the third one but incorporated loss rates. We will often refer to the first two replays as full replays and to the second two replays as collapsed-epochs replays.

It is important to note that our method for incorporating losses into the experiments, random dropping according to the measured probability of loss per connection, is not consistent with closed-loop traffic generation. We are by no means suggesting that loss rates should be incorporated in this manner into regular networking experiments that require closed-loop traffic generation. In such experiments, losses should only be the result of congestion on network links and buffering limitations. If this is the case, the endpoints generating synthetic traffic can not only react to the network conditions (e.g., reducing sending rates when congestion is detected), but also modify them (e.g., reducing overall congestion thanks to the lower sending rates). This is the right approach to reproduce the essential feedback loop in TCP which should be used in empirical studies of TCP performance.

However, loss is an important factor in TCP behavior (see Section 4.1.3), so our lossy experiments should result in a that is closer to the original . By incorporating losses, we eliminate one possible cause of divergence between original and replayed traces which could confuse our assessment of our source-level modeling approach. Comparing lossless and lossy replays enables a more systematic evaluation of our traffic modeling and generation methods, and it also helps to understand the impact of loss rates on the generated traffic. Losses are shown to have only a minimal effect on some traces and for some metrics, but a much more substantial effect on others.

The analysis in this section confirms the high-quality of the synthetic traffic generated using source-level trace replay. Our analysis reveals some (mostly minor) differences between original traffic and replay traffic. While we put forward some hypotheses about the cause of these differences, their confirmation requires further analysis. This additional work, which would involve both analysis and experimentation, would certainly be enlightening. It would tell us more about the limitations of our approach, and even about the inherent limitations of testbed experimentation. However, we have chosen not to pursue this avenue here. As discussed above, our goal is not to generate a equal to , but to convincingly demonstrate the benefits of our closed-loop traffic generation method. We believe this chapter achieves this goal, so we do not present any further analysis beyond the comparison of five traces and their four types of source-level replays using a rich set of metrics.