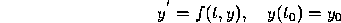



In preceding sections we have introduced the Euler formula, the improved Euler formula, and the three-term Taylor formula as ways to solve the initial value problem
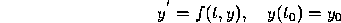
numerically. The local truncation errors for these methods are proportional
to 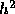 ,
, 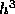 , and
, and 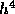 , respectively. All of these methods belong
to what is now called the Runge-Kutta class of methods.
, respectively. All of these methods belong
to what is now called the Runge-Kutta class of methods.
In this section we discuss the method originally developed by Runge and Kutta.
This method is now called the classic fourth order four-stage Runge-Kutta
method, but it is often referred to simply as the Runge-Kutta method,
and we will follow this practice for brevity. This method has a local
truncation error that is proportional to 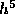 . Thus
it is two orders of magnitude more accurate than the improved Euler method and
the three-term Taylor method, and three orders of magnitude better than the
Euler formula. It is relatively simple to use and is sufficiently accurate to
handle many problems efficiently. This is especially true of adaptive
Runge-Kutta methods in which provision is made to vary the step size
as needed.
. Thus
it is two orders of magnitude more accurate than the improved Euler method and
the three-term Taylor method, and three orders of magnitude better than the
Euler formula. It is relatively simple to use and is sufficiently accurate to
handle many problems efficiently. This is especially true of adaptive
Runge-Kutta methods in which provision is made to vary the step size
as needed.
The Runge-Kutta formula involves a weighted average of values of
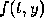 at different points in the interval
at different points in the interval 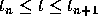 .
It is given by
.
It is given by
where
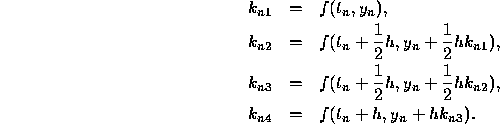
The sum 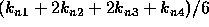 can be interpreted as an
average slope. Note that
can be interpreted as an
average slope. Note that 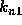 is the slope at the left end of the
interval,
is the slope at the left end of the
interval, 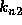 is the slope at the midpoint using the Euler formula to go
from
is the slope at the midpoint using the Euler formula to go
from 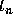 to
to 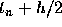 ,
,
 is a second approximation to the slope at the midpoint, and finally
is a second approximation to the slope at the midpoint, and finally
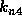 is the slope at
is the slope at 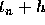 using the Euler formula and the slope
using the Euler formula and the slope
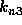 to go from
to go from 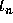 to
to 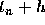 .
.
While in principle it is not difficult to show that Eq. (3) differs
from the Taylor expansion of the solution 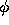 by terms that are
proportional to
by terms that are
proportional to 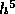 , the algebra is rather lengthy. Thus we will accept
the fact that the local truncation error in using Eq. (3) is
proportional to
, the algebra is rather lengthy. Thus we will accept
the fact that the local truncation error in using Eq. (3) is
proportional to 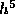 and that for a finite interval the global truncation
error is at most a constant times
and that for a finite interval the global truncation
error is at most a constant times 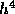 .
.
Clearly the Runge-Kutta formula, Eqs. (3), is more complicated than any of the formulas discussed previously. This is of relatively little significance, however, since it is not hard to write a computer program to implement this method. Such a program has the same structure as the algorithm for the Euler method.
Note that if f does not depend on y, then
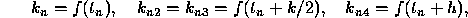
and Eq. (3) reduces to
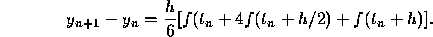
This equation can be identified as Simpson's rule for the approximate
evaluation of the integral of 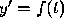 . The fact that Simpson's
rule has an error proportional to
. The fact that Simpson's
rule has an error proportional to 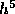 is consistent with the
local truncation error in the Runge-Kutta formula.
is consistent with the
local truncation error in the Runge-Kutta formula.


